题目内容
观察,计算,判断:(只填写符号:>,<,=)
(1)当a=2,b=2时,
与
的大小关系是
(2)当a=3,b=3时,
与
的大小关系是
(3)当a=4,b=4时,
与
的大小关系是
(4)当a=4,b=1时,
与
的大小关系是
(5)当a=5,b=3时,
与
的大小关系是
(6)当a=7,b=6时,
与
的大小关系是
…
写出关于
与
之间数量关系的猜想:
≥
≥
.
探究证明:(提示:(
-
)2≥0)
实践应用:要制作面积为1平方米的长方形镜框,直接利用探究得出的结论,求出镜框周长的最小值.
(1)当a=2,b=2时,
| a+b |
| 2 |
| ab |
=
=
.(2)当a=3,b=3时,
| a+b |
| 2 |
| ab |
=
=
.(3)当a=4,b=4时,
| a+b |
| 2 |
| ab |
=
=
.(4)当a=4,b=1时,
| a+b |
| 2 |
| ab |
>
>
.(5)当a=5,b=3时,
| a+b |
| 2 |
| ab |
>
>
.(6)当a=7,b=6时,
| a+b |
| 2 |
| ab |
>
>
.…
写出关于
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
探究证明:(提示:(
| a |
| b |
实践应用:要制作面积为1平方米的长方形镜框,直接利用探究得出的结论,求出镜框周长的最小值.
分析:(1)-(6)分别代入数据进行计算即可得解;
探究证明:根据非负数的性质,(
-
)2≥0,再利用完全平方公式展开整理即可得证;
实践应用:镜框为正方形时,周长最小,然后根据正方形的面积求出边长,即可得解.
探究证明:根据非负数的性质,(
| a |
| b |
实践应用:镜框为正方形时,周长最小,然后根据正方形的面积求出边长,即可得解.
解答:解:(1)当a=2,b=2时,
=
=2,
=
=2,
=
;
(2)当a=3,b=3时,
=
=3,
=
=3,
=
;
(3)当a=4,b=4时,
=
=4,
=
=4,
=
;
(4)当a=4,b=1时,
=
=
,
=
=2,
>
;
(5)当a=5,b=3时,
=
=4,
=
=
,
>
;
(6)当a=7,b=6时,
=
=6.5,
=
<6.5,
>
;
…
猜想:
≥
;
探究证明:根据非负数的性质(
-
)2≥0,
∴a-2
+b≥0,
整理得,
≥
;
实践应用:面积为1平方米的长方形镜框长与宽相等,即为正方形时,周长最小,
所以,边长为1,
周长为1×4=4.
| a+b |
| 2 |
| 2+2 |
| 2 |
| ab |
| 2×2 |
| a+b |
| 2 |
| ab |
(2)当a=3,b=3时,
| a+b |
| 2 |
| 3+3 |
| 2 |
| ab |
| 3×3 |
| a+b |
| 2 |
| ab |
(3)当a=4,b=4时,
| a+b |
| 2 |
| 4+4 |
| 2 |
| ab |
| 4×4 |
| a+b |
| 2 |
| ab |
(4)当a=4,b=1时,
| a+b |
| 2 |
| 4+1 |
| 2 |
| 5 |
| 2 |
| ab |
| 4×1 |
| a+b |
| 2 |
| ab |
(5)当a=5,b=3时,
| a+b |
| 2 |
| 5+3 |
| 2 |
| ab |
| 5×3 |
| 15 |
| a+b |
| 2 |
| ab |
(6)当a=7,b=6时,
| a+b |
| 2 |
| 7+6 |
| 2 |
| ab |
| 7×6 |
| a+b |
| 2 |
| ab |
…
猜想:
| a+b |
| 2 |
| ab |
探究证明:根据非负数的性质(
| a |
| b |
∴a-2
| ab |
整理得,
| a+b |
| 2 |
| ab |
实践应用:面积为1平方米的长方形镜框长与宽相等,即为正方形时,周长最小,
所以,边长为1,
周长为1×4=4.
点评:本题考查了二次根式的应用,准确进行运算判断出两个算式的大小关系是解题的关键.

练习册系列答案
相关题目


 某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了尚不完善的统计表,并计算了甲成绩的平均数和方差(见小宇的作业).
某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了尚不完善的统计表,并计算了甲成绩的平均数和方差(见小宇的作业). 与
与 的大小关系是______.
的大小关系是______.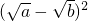 ≥0)
≥0) 与
与 的大小关系是______.
的大小关系是______. 与
与 的大小关系是______.
的大小关系是______. 与
与 的大小关系是______.
的大小关系是______. 与
与 的大小关系是______.
的大小关系是______. 与
与 的大小关系是______.
的大小关系是______. 与
与 的大小关系是______.
的大小关系是______. 与
与 之间数量关系的猜想:______
之间数量关系的猜想:______