题目内容
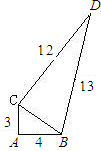一块试验田的形状如图所示，已知：∠CAB=90°，AC=3m，AB=4m，BD=13m，DC=12m．求这块试验田的面积．
解：∵∠CAB=90°，AC=3m，AB=4m，
∴BC=
=
=5m，
又∵52+122=132，即BC2+CD2=BD2，
∴△BCD为直角三角形，
S△ABC=
×AB×AC=×4×3=6，
S△BCD=×BC×CD=×5×12=30，
故这块试验田的面积=S△ABC+S△BCD=36m2．
分析：根据题中的已知条件，运用勾股定理的逆定理可证△BCD为直角三角形，代入三角形的面积公式可将两个直角三角形的面积求解出来，两个直角三角形的面积和即为此块试验田的面积．
点评：本题主要是运用勾股定理的逆定理证明△BCD为直角三角形．
∴BC=
==5m，又∵52+122=132，即BC2+CD2=BD2，
∴△BCD为直角三角形，
S△ABC=
×AB×AC=×4×3=6，S△BCD=
×BC×CD=×5×12=30，故这块试验田的面积=S△ABC+S△BCD=36m2．
分析：根据题中的已知条件，运用勾股定理的逆定理可证△BCD为直角三角形，代入三角形的面积公式可将两个直角三角形的面积求解出来，两个直角三角形的面积和即为此块试验田的面积．
点评：本题主要是运用勾股定理的逆定理证明△BCD为直角三角形．
练习册系列答案
阅读快车系列答案
相关题目
6、如图所示，一块试验田的形状是三角形（设其为△ABC），管理员从BC边上的一点D出发，沿DC?CA?AB?BD的方向走了一圈回到D处，则管理员从出发到回到原处在途中身体（ ）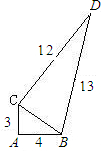
一块试验田的形状如图所示，已知：∠CAB=90°，AC=3m，AB=4m，BD=13m，DC=12m．求这块试验田的面积．
如图，一块试验田的形状是三角形（设其为△ABC），管理员从BC边上的一点D出发，沿DC→CA→AB→BD的方向走了一圈回到D处，则管理员从出发到回到原处在途中身体转过
一块试验田的形状如图，已知：∠ABC=90°，AB=4m，BC=3m，AD=12m，CD=13m．求这块试验田的面积．