题目内容
如图，已知AC和BD相交于点E，CE•AE=BE•DE，求证：△ABE∽△DCE．
解：∵CE•AE=BE•DE，
∴
∵∠AEB=∠DEC
∴△ABE∽△DCE．
分析：利用两组对应边的比相等且夹角相等判定两三角形相似即可．
点评：本题考查了相似三角形的判定，解题的关键是熟练掌握相似三角形的判定方法．
∴
∵∠AEB=∠DEC
∴△ABE∽△DCE．
分析：利用两组对应边的比相等且夹角相等判定两三角形相似即可．
点评：本题考查了相似三角形的判定，解题的关键是熟练掌握相似三角形的判定方法．
练习册系列答案
相关题目
3、如图，已知AC和BD相交于O点，AD∥BC，AD=BC，过O任作一条直线分别交AD，BC于点E，F，则下列结论：①OA=OC ②OE=OF ③AE=CF ④OB=OD，其中成立的个数是（ ）
20、如图，已知AC和BD相交于O，且BO=DO，AO=CO，下列判断正确的是（ ）
18、如图，已知AC和BD相交于O点，AD∥BC，AD=BC，过O任作一条直线分别交AD，BC于点E、F，则OE
如图，已知AC和BD相交于点E，CE•AE=BE•DE，求证：△ABE∽△DCE．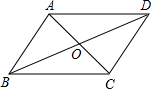
如图，已知AC和BD相交于O，且BO=DO，AO=CO．求证：△AOB≌△COD．