题目内容
已知双曲线![]() 与直线
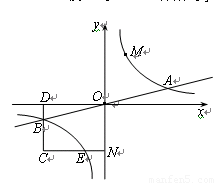
与直线![]() 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线![]() 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线![]() 于点E,交BD于点C.
于点E,交BD于点C.

1.若点D坐标是(-8,0),求A、B两点坐标及k的值.
2.若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
1.∵D(-8,0),∴B点坐标为(-8,-2).…………………………1分
而A、B两点关于原点对称,∴A(8,2).………………………………………2分
从而![]() .……………………………………………………………… 3分
.……………………………………………………………… 3分
2.∵N(0,-n),B是CD的中点,A、B、M、E四点均在双曲线上,∴![]() ,B(-2m,-
,B(-2m,-![]() ),C(-2m,-n),E(-m,-n). S矩形DCNO
),C(-2m,-n),E(-m,-n). S矩形DCNO![]() ,S△DBO=
,S△DBO=![]() ,S△OEN =
,S△OEN =![]() , ∴S四边形OBCE= S矩形DCNO-S△DBO- S△OEN=k.∴
, ∴S四边形OBCE= S矩形DCNO-S△DBO- S△OEN=k.∴![]() .……………………………………4分,
.……………………………………4分,
得A(4,1),B(-4,-1),
∴C(-4,-2),M(2,2).…………………………………………………………5分
设![]() ,解得
,解得 .∴
.∴![]() .……………………………………6分
.……………………………………6分
解析:(1)从D点的坐标和直线方程求出B点坐标,再通过A、B两点关于原点对称得出A点坐标,把A点坐标代入反比例函数中得出k的值;
(2)利用四边形OBCE的面积解出k的值,再求出双曲线与直线的两交点A、B的坐标,
根据B是CD的中点得出C点坐标,再得出M点的坐标,利用两点式解出直线CM的解析式

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
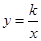 与直线
与直线 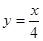 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线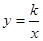 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线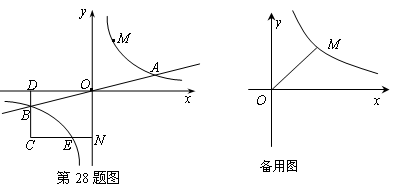
 与直线
与直线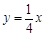 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线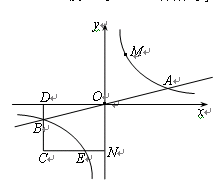
 与直线
与直线 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
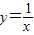 与直线y=x-
与直线y=x-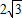 相交于点P(a,b),则
相交于点P(a,b),则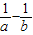 .
.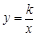 与直线
与直线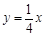 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线