题目内容
12．
如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为50和38，则△EDF的面积为6．
分析 过点D作DH⊥AC于H，根据角平分线上的点到角的两边距离相等可得DF=DH，然后利用“HL”证明Rt△DEF和Rt△DGH全等，根据全等三角形的面积相等可得S△EDF=S△GDH，设面积为S，然后根据S△ADF=S△ADH列出方程求解即可．
解答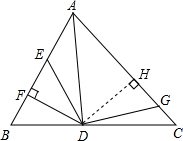 
解：如图，过点D作DH⊥AC于H，
∵AD是△ABC的角平分线，DF⊥AB，
∴DF=DH，
在Rt△DEF和Rt△DGH中，
$\left\{\begin{array}{l}{DE=DG}\\{DF=DH}\end{array}\right.$，
∴Rt△DEF≌Rt△DGH（HL），
∴S△EDF=S△GDH，设面积为S，
同理Rt△ADF≌Rt△ADH，
∴S△ADF=S△ADH，
即38+S=50-S，
解得S=6．
故答案为：6．
点评 本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，作辅助线构造出全等三角形并利用角平分线的性质是解题的关键．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
2．等腰三角形的周长为12cm，其中一边长为5cm，则该等腰三角形的底边为（ ）
| A． | 5cm | B． | 3cm | C． | 3.5cm或2cm | D． | 8cm |
3．关于代数式$\frac{{a}^{2}-3b}{2}$，下列表述正确的是（ ）
| A． | 单项式，次数为1 | B． | 单项式，次数为2 | C． | 多项式，次数为2 | D． | 多项式，次数为3 |
17．下表是国外城市与北京的时差 （带正号的数表示同一时刻比北京时间早的时数）
如果现在东京时间是16：00，那么纽约时间是2：00．（以上均为24小时制）
| 城市 | 纽约 | 巴黎 | 东京 | 多伦多 |
| 时差（时） | -13 | -7 | +1 | -12 |
