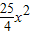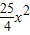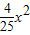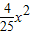题目内容
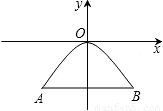
如图1是抛物线形的拱桥，当水面在l时，拱顶离水面2米，水面宽4米．
（1）借助图2的直角坐标系，求此抛物线的解析式；
（2）当水面下降1米时，求水面宽增加了多少米？
解：如图，建立直角坐标，
可设这条抛物线为y=ax2，
把点（2，-2）代入，得
-2=a×22，a=-
，
∴y=-，
∴此抛物线的解析式为：y=-x2；
（2）∵当水面下降1米时，
即当y=-3时，-3=-x2，
解得：x=±
，
∴水面下降1m，水面宽度增加（2-4）m．
分析：（1）根据建立的直角坐标系，设抛物线为y=ax2，把点（2，-2）代入求出解析式可解；
（2）利用（1）中所求解析式，进而将y=-3代入求出水面宽度，即可得出水面宽度增加的值．
点评：此题主要考查了二次函数的应用，根据已知图象假设出解析式，进而求出是解题关键．
可设这条抛物线为y=ax2，
把点（2，-2）代入，得
-2=a×22，a=-
，∴y=-
，∴此抛物线的解析式为：y=-
x2；（2）∵当水面下降1米时，
即当y=-3时，-3=-
x2，解得：x=±
，∴水面下降1m，水面宽度增加（2
-4）m．分析：（1）根据建立的直角坐标系，设抛物线为y=ax2，把点（2，-2）代入求出解析式可解；
（2）利用（1）中所求解析式，进而将y=-3代入求出水面宽度，即可得出水面宽度增加的值．
点评：此题主要考查了二次函数的应用，根据已知图象假设出解析式，进而求出是解题关键．
练习册系列答案
相关题目
如图所示，桥拱是抛物线形，其函数的表达式为y=-| 1 |
| 4 |
| A、3m | ||
B、2
| ||
C、4
| ||
| D、9m |
如图所示，桥拱是抛物线形，其函数解析式是y=-
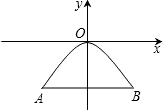如图所示是一个抛物线形桥拱的示意图，在所给出的平面直角坐标系中，当水位在AB位置时，水面宽度为10m，此时水面到桥拱的距离是4m，则抛物线的函数关系式为（ ）A、y=
| ||
B、y=-
| ||
C、y=-
| ||
D、y=
|
19、如图是把一个抛物线形桥拱，量得两个数据，画在纸上的情形．小明说只要建立适当的坐标系，就能求出此抛物线的表达式．你认为他的说法正确吗？如果不正确，请说明理由；如果正确，请你帮小明求出该抛物线的表达式．
