题目内容
如图是某公园一圆形喷水池,水流在各个方向沿形状相同的抛物线落下,建立如图所示的坐标系,如果喷头所在处A(0,1.25),水流路线最高处M(1,2.25),如果不考虑其他因素,那么水池的半径至少要 m,才能使喷出的水流不至落到池外.
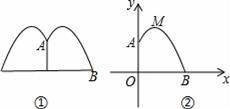

2.5
【考点】二次函数的应用.
【分析】所谓的水池半径即为抛物线与x轴交点的横坐标,设出抛物线方程,代入已知点即可得出结论.
【解答】解:∵M(1,2.25)为抛物线的顶点,
∴设抛物线方程为:y=a(x﹣1)2+2.25,
∵点A(0,1.25)为抛物线上的一个点,
∴1.25=a(0﹣1)2+2.25,
解得:a=﹣1,
∴抛物线方程为:y=﹣(x﹣1)2+2.25,
将y=0代入抛物线方程得:0=﹣(x﹣1)2+2.25,
解得:x1=2.5,x2=﹣0.5(舍去),
故答案为:2.5.
【点评】本题考查的是抛物线方程得顶点式的运用,解题的关键是明白所求的半径为抛物线与x轴正半轴的交点坐标.

练习册系列答案
相关题目






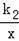
 (x>0)的图象交于A(1,6),B(a,3)两点.
(x>0)的图象交于A(1,6),B(a,3)两点.
