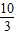题目内容
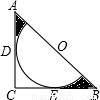
(2003•荆州)如图,等腰三角形△ABC中,∠C=90°,AB=4,O是AB的中点,以O为圆心的半圆分别与两腰相切点D,E,则图中阴影部分的面积是 (结果用π表示).
【答案】分析:连接OD,那么△ABC上边的阴影部分的面积可用△AOD和△AOD内部的扇形的面积差来得出,同理可求出△ABC下边的阴影部分的面积.由此可得出所求的结果.
解答: 解:连接OD,则OD⊥AC,△AOD为等腰直角三角形,
解:连接OD,则OD⊥AC,△AOD为等腰直角三角形,
又AB=4,O是AB的中点,∴OA=2;OD=
∴△AOD中的阴影面积= ×2×1-
×2×1- =1-
=1- ;
;
同理△AOD中的阴影面积=1- ;
;
则图中阴影部分的面积是2- .
.
点评:此题综合考查切线的性质、等腰直角三角形的性质和扇形的面积计算.
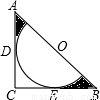
解答:
 解:连接OD,则OD⊥AC,△AOD为等腰直角三角形,
解:连接OD,则OD⊥AC,△AOD为等腰直角三角形,又AB=4,O是AB的中点,∴OA=2;OD=

∴△AOD中的阴影面积=
 ×2×1-
×2×1- =1-
=1- ;
;同理△AOD中的阴影面积=1-
 ;
;则图中阴影部分的面积是2-
 .
.点评:此题综合考查切线的性质、等腰直角三角形的性质和扇形的面积计算.

练习册系列答案
相关题目
 <y<24.
<y<24.
 <y<24.
<y<24.
 BF,若BC=10,那么DC的长是( )
BF,若BC=10,那么DC的长是( )