题目内容
△ABC中，AC=6，AB=BC=5，则BC边上的高AD=
．
| 24 |
| 5 |
| 24 |
| 5 |
分析：先根据题意画出图形，由等腰三角形的性质可求出AE的长，根据勾股定理求出BE的长，由三角形的面积公式即可得出AD的长．
解答：
解：如图所示：过点B作BE⊥AC于点E，
∵AC=6，AB=BC=5，
∴AE=
AC=3，
∴在Rt△ABE中，BE=
=
=4，
∴
AC•BE=
BC•AD，即AD=
=
=
．
故答案为：
．
解：如图所示：过点B作BE⊥AC于点E，∵AC=6，AB=BC=5，
∴AE=
| 1 |
| 2 |
∴在Rt△ABE中，BE=
| AB2-AE2 |
| 52-32 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| AC•BE |
| BC |
| 6×4 |
| 5 |
| 24 |
| 5 |
故答案为：
| 24 |
| 5 |
点评：本题考查的是勾股定理及等腰三角形的性质，熟知等腰三角形三线合一的性质是解答此题的关键．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
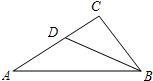如图，在△ABC中，AC＞BC，D是AC边上一点，连接BD．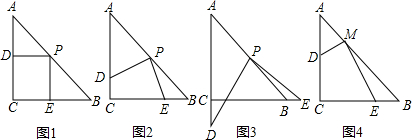
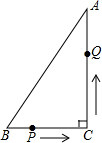如图，在Rt△ABC中，AC=24cm，BC=7cm，P点在BC上，从B点到C点运动（不包括C点），点P运动的速度为2cm/s；Q点在AC上从C点运动到A点（不包括A点），速度为5cm/s．若点P、Q分别从B、C同时运动，且运动时间记为t秒，请解答下面的问题，并写出探索的主要过程．