题目内容
已知D、E分别在△ABC的BA、CA的延长线上,下列给出的条件中能判定ED∥BC的是
- A.
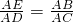
- B.

- C.
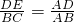
- D.

B
分析:根据选项选出能推出△DAE∽△BAC,推出∠D=∠B或∠E=∠C的即可.
解答:
A、∵ =
= ,
,
∴ =
= ,
,
∵∠EAD=∠BAC,
∴△EAD∽△BAC,
∴∠E=∠B,∠D=∠C,
即不能推出DE∥BC,故本选项错误;
B、∵ =
= ,
,
∴ =
= ,
,
∴ -1=
-1= -1,
-1,
∴ =
= ,
,
∵∠EAD=∠BAC,
∴△DAE∽△BAC,
∴∠D=∠B,
∴DE∥BC,故本选项正确;
C、 =
= 不能推出△DAE∽△BAC,即不能推出∠D=∠B,即不能推出两直线平行,故本选项错误;
不能推出△DAE∽△BAC,即不能推出∠D=∠B,即不能推出两直线平行,故本选项错误;
D、 =
=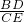 不能推出△DAE∽△BAC,即不能推出∠D=∠B,即不能推出两直线平行,故本选项错误;
不能推出△DAE∽△BAC,即不能推出∠D=∠B,即不能推出两直线平行,故本选项错误;
故选B.
点评:本题考查了相似三角形的性质和判定和平行线的判定的应用,主要考查学生的推理和辨析能力,注意:有两组对应边的比相等,且这两边的夹角相等的两三角形相似.
分析:根据选项选出能推出△DAE∽△BAC,推出∠D=∠B或∠E=∠C的即可.
解答:

A、∵
 =
= ,
,∴
 =
= ,
,∵∠EAD=∠BAC,
∴△EAD∽△BAC,
∴∠E=∠B,∠D=∠C,
即不能推出DE∥BC,故本选项错误;
B、∵
 =
= ,
,∴
 =
= ,
,∴
 -1=
-1= -1,
-1,∴
 =
= ,
,∵∠EAD=∠BAC,
∴△DAE∽△BAC,
∴∠D=∠B,
∴DE∥BC,故本选项正确;
C、
 =
= 不能推出△DAE∽△BAC,即不能推出∠D=∠B,即不能推出两直线平行,故本选项错误;
不能推出△DAE∽△BAC,即不能推出∠D=∠B,即不能推出两直线平行,故本选项错误;D、
 =
=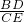 不能推出△DAE∽△BAC,即不能推出∠D=∠B,即不能推出两直线平行,故本选项错误;
不能推出△DAE∽△BAC,即不能推出∠D=∠B,即不能推出两直线平行,故本选项错误;故选B.
点评:本题考查了相似三角形的性质和判定和平行线的判定的应用,主要考查学生的推理和辨析能力,注意:有两组对应边的比相等,且这两边的夹角相等的两三角形相似.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 25、如图,已知D、E分别在AC、AB上,BD、CE相交于点O,且AB=AC,∠1=∠2.
25、如图,已知D、E分别在AC、AB上,BD、CE相交于点O,且AB=AC,∠1=∠2. (2013•宜宾)如图:已知D、E分别在AB、AC上,AB=AC,∠B=∠C,求证:BE=CD.
(2013•宜宾)如图:已知D、E分别在AB、AC上,AB=AC,∠B=∠C,求证:BE=CD.