Question

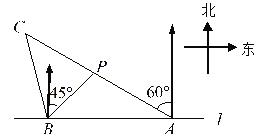
【题目】如图，抛物线与轴交于点，与轴交于、两点，其中、是方程的两根，且．

（）求抛物线的解析式；

（）直线上是否存在点，使为直角三角形．若存在，求所有点坐标；反之说理；

（）点为轴上方的抛物线上的一个动点（点除外），连、，若设的面积为． 点横坐标为，则在何范围内时，相应的点有且只有个．

Answer 1

【答案】（）；（）；（3）.

【解析】试题分析：（1）解方程求得抛物线与x轴交点的横坐标，再用待定系数法求抛物线的解析式即可；（2）用待定系数法求得直线AC的解析式，再分①∠DBC=90°、②∠DBC=90°两种情况求点D的坐标即可；（3）求得点P在抛物线AB段上时S的最大值，再求得点P在抛物线AC段上时，S的最大值，即可得S的取值范围.

试题解析：

（），

， ，

设，

把代入得， ，

解得．

∴

．

（）设直线AC的解析式为y=kx+b，将A、C两点坐标代入得，

，

解得 ,k=,b=4 ,

∴．

①∠BDC=90°时，

．

， ，

∴．

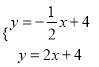②∠DBC=90°时，x=-2，y=-×（-2）+4=5，则D点坐标为（-2，5）；

∴， ．

（3）点P在抛物线AC段上时S最大值为16，点P在抛物线AB段上时S最大值为20，

则S的取值范围为16＜S＜20．