题目内容
【题目】如图,在![]() 中,
中,![]() 于点
于点![]() . 点
. 点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向点
向点![]() 运动,点
运动,点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向点
向点![]() 运动,两点同时出发,速度都为每秒1个单位长度,当点
运动,两点同时出发,速度都为每秒1个单位长度,当点![]() 运动到
运动到![]() 时,两点都停止. 设运动时间为
时,两点都停止. 设运动时间为![]() 秒.
秒.
(1)求线段![]() 的长;
的长;
(2)当![]() 为何值时,
为何值时,![]() 是直角三角形?
是直角三角形?
(3)是否存在某一时刻,使得![]() 分
分![]() 的面积为1:11?若存在,求出
的面积为1:11?若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】(1)![]() ;
;
(2)![]() 为3秒或
为3秒或![]() 秒时,
秒时,![]() 是直角三角形;
是直角三角形;
(3)当![]() 时使得
时使得![]() 分
分![]() 的面积为1:11.
的面积为1:11.
【解析】
(1)利用勾股定理可求出AB长,再用等积法就可求出线段CD的长,
(2)先用t表示出DP,CQ,CP的长,再分PQ⊥CD与PQ⊥AC两种情况进行讨论;
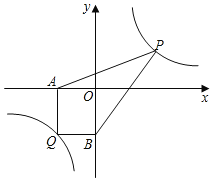
(3)过点![]() 作
作![]() 于
于![]() ,通过三角形相似即可用t的代数式表示QE,从而可以求出
,通过三角形相似即可用t的代数式表示QE,从而可以求出![]() 和
和![]() ;利用
;利用![]() 分
分![]() 的面积为1:11,分两种情况讨论,①
的面积为1:11,分两种情况讨论,① ![]() ,②
,②![]() ,建立t的方程,解方程即可解决问题.
,建立t的方程,解方程即可解决问题.
解:(1)在![]() 中,根据勾股定理得,
中,根据勾股定理得,![]() ,
,
∵![]() ,
,
∴![]() ,
,
(2)由(1)知,![]() ,由运动知,
,由运动知,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是直角三角形,
是直角三角形,
∴①
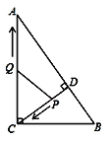
当PQ⊥CD时,如图a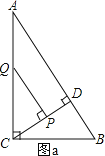
∴![]() ,
,
∴![]() ,
,
∴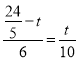 ,
,
∴![]()
②当PQ⊥AC,如图b.
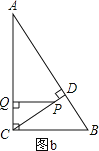
∴![]() ,
,
∴![]() ,
,
∴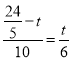
∴![]() ,
,
即:![]() 为3秒或
为3秒或![]() 秒时,
秒时,![]() 是直角三角形
是直角三角形
(3)假设存在,如图,
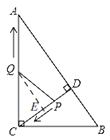
在![]() 中,根据勾股定理得,
中,根据勾股定理得,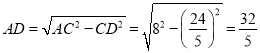 ,
,
过点![]() 作
作![]() 于
于![]() ,
,
∴,
∴![]() ,
,
∴![]() ,
,
∴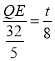 ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∵![]() 分
分![]() 的面积为1:11,
的面积为1:11,
∴①当![]() 时,
时,
∴![]() ,
,
∴![]() ,
,
解得![]() ,
,
②当![]() 时,
时,
![]() ,
,
∴![]() ,
,
而![]() ,
,
此方程无解,即:此种情况不存在,
综上所述,当![]() 时使得
时使得![]() 分
分![]() 的面积为1:11.
的面积为1:11.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目