题目内容
在平行四边形ABCD中,∠A﹦80°,则∠B= .
考点:平行四边形的性质
专题:
分析:在平行四边形ABCD中,因为∠A和∠B是一组相邻的内角,由平行四边形的性质可知,∠A+∠B=180°,代值求解.
解答:解:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠A+∠B=180°,
∴∠B=180°-∠A
=180°-80°=100°.
故答案为100°.
∴BC∥AD,
∴∠A+∠B=180°,
∴∠B=180°-∠A
=180°-80°=100°.
故答案为100°.
点评:本题利用了平行四边形中邻角互补的性质.运用平行四边形的性质可解决以下问题,如求角的度数、线段的长度,证明角相等或互补,证明线段相等或倍分等.

练习册系列答案
相关题目
若y=kx-4的函数值y随着x的增大而减小,则k的值可能是下列的( )
| A、π | ||
B、
| ||
| C、0 | ||
| D、-4 |
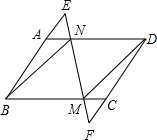 如图,在平行四边形ABCD中,延长BA到点E,延长DC到点F,使AE=CF,连接EF,分别交AD、BC于点N、M,连接BN、DM.
如图,在平行四边形ABCD中,延长BA到点E,延长DC到点F,使AE=CF,连接EF,分别交AD、BC于点N、M,连接BN、DM. 有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B的面积之和为
有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B的面积之和为 如图,点A为x轴上一点,坐标为(4,0),点B、点C为y轴上两点,点B的坐标为(0,6),连接AB,过点C作x轴的平行线CD交AB于D,若S△BCD=
如图,点A为x轴上一点,坐标为(4,0),点B、点C为y轴上两点,点B的坐标为(0,6),连接AB,过点C作x轴的平行线CD交AB于D,若S△BCD= 如图,在△ABC中,∠A=80°,∠B=60°,将△ABC沿EF对折,点C落在C′处.如果∠1=50°,那么∠2=
如图,在△ABC中,∠A=80°,∠B=60°,将△ABC沿EF对折,点C落在C′处.如果∠1=50°,那么∠2=