题目内容
如图,⊙ 是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙
是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙ 于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF。
于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF。
(1)若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)
(2)求证:OD=OE;
(3)PF是⊙ 的切线。
的切线。

(1)解:由直径AC=12得半径OC=6
劣弧PC的长为
(2)证明:∵ OD⊥AB,PE⊥AC

 ∴ ∠ADO=∠PEO=90°
∴ ∠ADO=∠PEO=90°
在△ADO和△PEO中,

∴ △ADO≌△PEO
∴ OD=OE
(3)解:连接PC,由AC是直径知BC⊥AB,又OD⊥AB,
∴ PD∥BF
∴ ∠OPC=∠PCF,∠ODE=∠CFE
由(2)知OD=OE,则∠ODE=∠OED,又∠OED=∠FEC
∴ ∠FEC=∠CFE
∴ EC=FC
由OP=OC知∠OPC=∠OCE
∴ ∠PCE =∠PCF
在△PCE和△PFC中,

∴ △PCE≌△PFC
∴ ∠PFC =∠PEC=90°
由∠PDB=∠B=90°可知∠ODF=90°即OP⊥PF
∴ PF是⊙ 的切线
的切线

练习册系列答案
相关题目
 23,25 B. 24,23
23,25 B. 24,23 D. 23,24
D. 23,24

 是同类二次根式的是
是同类二次根式的是 B.
B. C.
C. D.
D.
 的三个结论:①它的图象经过点(7,3);②它的图象在每一个象限内,
的三个结论:①它的图象经过点(7,3);②它的图象在每一个象限内, 随
随 的增大而减小;③它的图象在二、四象限内.其中正确的是________________.
的增大而减小;③它的图象在二、四象限内.其中正确的是________________.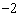 C.6 D.
C.6 D.
 和点
和点 都在反比例函数
都在反比例函数 的图象上,
的图象上,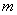
 (填“
(填“ ”、“
”、“ ” 或“
” 或“ ”号)
”号)