题目内容
如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为 x米,面积为S平方米.
x米,面积为S平方米.
(1)求S与x的函数关系式及自变量x的取值范围;
(2)若墙的最大可用长度为9米,求此时自变量x的取值范围.
 x米,面积为S平方米.
x米,面积为S平方米.(1)求S与x的函数关系式及自变量x的取值范围;
(2)若墙的最大可用长度为9米,求此时自变量x的取值范围.
分析:(1)花圃的面积=AB×(篱笆长-3AB),根据边长为正数可得自变量的取值范围;
(2)结合(1)及AD不大于9可得自变量的公共取值.
(2)结合(1)及AD不大于9可得自变量的公共取值.
解答:解:(1)S=BC×AB=(24-3x)x=-3x2+24x
由题意得:
0<x<8
(2)∵24-3x≤9
∴x≥5
结合(1)得,5≤x<8.
由题意得:
|
0<x<8
(2)∵24-3x≤9
∴x≥5
结合(1)得,5≤x<8.
点评:考查一次函数的应用;得到AD边长的关系式是解决本题的突破点;得到自变量的取值是解决本题的易错点.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
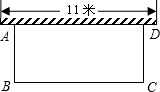 边不超过墙长),设与墙平行的一边BC的长为x米,面积为y平方米.
边不超过墙长),设与墙平行的一边BC的长为x米,面积为y平方米. 与墙平行的一边BC的长为x米,面积为y平方米.
与墙平行的一边BC的长为x米,面积为y平方米. 与墙平行的一边BC的长为x米,面积为y平方米.
与墙平行的一边BC的长为x米,面积为y平方米.
