题目内容
（2013•江都市一模）周末，小亮一家在瘦西湖游玩，妈妈在岸边P处观看小亮与爸爸在湖中划船（如图）．小船从P处出发，沿北偏东60°划行300米到达A处，接着向正南方向划行一段时间到达B处．在B处小亮观测妈妈所在的P处在北偏西37°方向上，这时小亮与妈妈相距多少米（精确到1米）？（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，| 2 |
| 3 |
分析：作PD⊥AB于点D，分别在直角三角形PAD和直角三角形PBD中求得PD和PB即可求得结论．
解答：解：作PD⊥AB于点D，
由已知得PA=300米，∠APD=30°，∠B=37°，
在Rt△PAD中，
由cos30°=
，得PD=PAcos30°=300×
=150
米，
在Rt△PBD中，
由sin37°=
，得PB=
≈433米．
答：小亮与妈妈的距离约为433米．
由已知得PA=300米，∠APD=30°，∠B=37°，
在Rt△PAD中，
由cos30°=
| PD |
| PA |
| ||
| 2 |
| 3 |
在Rt△PBD中，
由sin37°=
| PD |
| PB |
| PD |
| sin37° |
答：小亮与妈妈的距离约为433米．
点评：本题考查了解直角三角形的应用，解题的关键是从实际问题中整理出直角三角形并求解．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
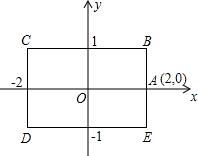（2013•江都市一模）如图，矩形BCDE的各边分别平行于x轴或y轴，物体甲和物体乙由点A（2，0）同时出发，沿矩形BCDE的边作环绕运动，物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2013次相遇地点的坐标是（ ）
（2013•江都市一模）如图，正方形网格中每个小正方形边长都是1，每个小格的顶点叫格点，以格点为顶点的三角形叫做格点三角形．