题目内容
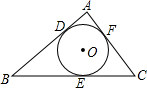
如图，⊙O内切△ABC于D、E、F，∠B=50°，∠C=60°，则∠FDE的度数为
- A.50°
- B.55°
- C.60°
- D.70°
B
分析：首先求出∠A的度数，再根据切线的性质定理以及四边形的内角和得出∠FOE的度数，进而得出∠FDE的度数．
解答：
解：连接OE，OF，
∵∠B=50°，∠C=60°，
∴∠A=180°-50°-60°=70°，
∵⊙O内切△ABC于D、E、F，
∴∠AFO=∠AEO=90°，
∴∠FOE=180°-∠A=180°-70°=110°，
∴∠FDE=
∠FOE=55°．
故选：B．
点评：本题考查了三角形的内切圆与内心，综合运用了圆周角定理以及切线的性质定理和四边形的内角和定理得出∠FOE的度数是解题关键．
分析：首先求出∠A的度数，再根据切线的性质定理以及四边形的内角和得出∠FOE的度数，进而得出∠FDE的度数．
解答：
解：连接OE，OF，∵∠B=50°，∠C=60°，
∴∠A=180°-50°-60°=70°，
∵⊙O内切△ABC于D、E、F，
∴∠AFO=∠AEO=90°，
∴∠FOE=180°-∠A=180°-70°=110°，
∴∠FDE=
∠FOE=55°．故选：B．
点评：本题考查了三角形的内切圆与内心，综合运用了圆周角定理以及切线的性质定理和四边形的内角和定理得出∠FOE的度数是解题关键．
练习册系列答案
相关题目
如图，⊙O内切于Rt△ABC，∠C=Rt∠，D、E、F是切点，若∠BOC=105°，AB=4cm，则∠OBC=
如图：⊙O内切于弓形ADB的最大的圆，且弧ADB的度数为120°，则⊙O的周长与弧AB的长的比是
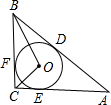
已知如图，△ABC内切⊙O于D、E、F三点，内切圆⊙O的半径为1，∠C=60°，AB=5，则△ABC的周长为（ ）| A、12 | ||
| B、14 | ||
C、10+2
| ||
D、10+
|
如图，⊙O内切于△ABC，切点分别为D、E、F，且DE∥BC，若AB=8cm，AD=5cm，则△ADE的周长是
如图，⊙O内切于△ABC，切点依次为D、E、F，若AB=5，BC=7，AC=8，那么AD=