题目内容
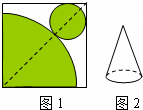如图1，在正方形铁皮上剪下一个圆形和扇形，使之恰好围成图2所示的一个圆锥模型．设圆的半径为r，扇形半径为R，则圆的半径r与扇形半径R之间的关系为分析：根据围成圆锥后圆锥的侧面展开扇形的弧长等于圆锥的底面周长，列出关系式即可得到两个半径之间的关系．
解答：解：∵恰好围成图2所示的一个圆锥模型，
∴圆锥的侧面展开扇形的弧长等于圆锥的底面周长，
∴
=2πr，
解得：R=4r或r=
故答案为：R=4r或r=
∴圆锥的侧面展开扇形的弧长等于圆锥的底面周长，
∴
| 90π×R |
| 180 |
解得：R=4r或r=
| R |
| 4 |
故答案为：R=4r或r=
| R |
| 4 |
点评：本题考查了圆锥的计算，解决本题的关键是利用题目已知条件得到扇形的弧长和圆的周长之间的关系，并利用其列出关系式．
练习册系列答案
相关题目
如图1，在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形，使之恰好围成图2所示的一个圆锥，则圆锥的高为（ ）A、
| ||
| B、4cm | ||
C、
| ||
D、
|
如图1，在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形，使之恰好围成图2所示的一个圆锥，求圆锥的高．
如图(1)，在正方形铁皮上剪下一个圆形和扇形，使之恰好围成图(2)所示的一个圆锥模型，则圆的半径r与扇形的半径R之间的关系为 ( )
| A．R＝2r | B．R＝ r |
| C．R＝3r | D．R＝4r |
r