题目内容
 如图,在半径为2的扇形AOB中,∠AOB=90°,点C是
如图,在半径为2的扇形AOB中,∠AOB=90°,点C是 上的一个动点(不与点A、B重合),OD⊥BC,OE⊥AC,垂足分别为D、E.
上的一个动点(不与点A、B重合),OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=1时,求线段OD的长;
(2)在△DOE中是否存在长度不变的边?若存在,请指出并求其长度;如果不存在,请说明理由;
(3)求:S△ODE-S△CDE的值.
解:(1)∵OD⊥BC,
∴BD= BC=
BC=
而BC=2,
在RtOBD中,OD= =
= ;
;
(2)在△DOE中DE的长度不变.
 连结AB,如图,
连结AB,如图,
∵∠AOB=90°,OA=OB=2,
∴AB= OA=2
OA=2 ,
,
∵OD⊥BC,OE⊥AC,
∴DB=DC,EA=EC,即点D和E分别是线段BC和AC的中点,
∴DE为△CBA的中位线,
∴DE= AB=
AB= ;
;
(3)连结OC,
∵DE∥BA,
∴△CDE∽△CBA,
∴S△CDE:S△CBA=(CD:CB)2=1:4,即S△CBA=4S△CDE,
∵S△ODB=S△ODC,S△OAE=S△OEC,
∴S△ODE=S四边形ODCE-S△CDE,
=S△ODC+S△OEC-S△CDE
= S△OBC+
S△OBC+ S△OAC-S△CDE
S△OAC-S△CDE
= S四边形ODCE-S△CDE
S四边形ODCE-S△CDE
= S△OAB+
S△OAB+ S△CAB-S△CDE
S△CAB-S△CDE
= ×
× ×2×2+
×2×2+ ×4S△CDE-S△CDE
×4S△CDE-S△CDE
=1+S△CDE,
∴S△ODE-S△CDE=1.
分析:(1)根据垂径定理由OD⊥BC得BD= ,在Rt△BOD中利用勾股定理即可求出OD的长;
,在Rt△BOD中利用勾股定理即可求出OD的长;
(2)连接AB,根据等腰直角三角形的性质可得出AB=2 ,再根据垂径定理得到OD⊥BC,OE⊥AC,则DE为△CBA的中位线,然后根据三角形中位线性质即可得到DE=
,再根据垂径定理得到OD⊥BC,OE⊥AC,则DE为△CBA的中位线,然后根据三角形中位线性质即可得到DE= ;
;
(3)连结OC,由DE∥BA可判断△CDE∽△CBA,根据相似三角形的性质得S△CDE:S△CBA=(CD:CB)2=1:4,即S△CBA=4S△CDE,再利用S△ODB=S△ODC,S△OAE=S△OEC和S△ODE=S四边形ODCE-S△CDE进行变形可得到S△ODE-S△CDE的值.
点评:本题考查了圆的综合题:熟练掌握垂径定理;学会运用勾股定理和相似比进行几何计算;同时理解等腰直角三角形的性质.
∴BD=
 BC=
BC=
而BC=2,
在RtOBD中,OD=
 =
= ;
;(2)在△DOE中DE的长度不变.
 连结AB,如图,
连结AB,如图,∵∠AOB=90°,OA=OB=2,
∴AB=
 OA=2
OA=2 ,
,∵OD⊥BC,OE⊥AC,
∴DB=DC,EA=EC,即点D和E分别是线段BC和AC的中点,
∴DE为△CBA的中位线,
∴DE=
 AB=
AB= ;
;(3)连结OC,
∵DE∥BA,
∴△CDE∽△CBA,
∴S△CDE:S△CBA=(CD:CB)2=1:4,即S△CBA=4S△CDE,
∵S△ODB=S△ODC,S△OAE=S△OEC,
∴S△ODE=S四边形ODCE-S△CDE,
=S△ODC+S△OEC-S△CDE
=
 S△OBC+
S△OBC+ S△OAC-S△CDE
S△OAC-S△CDE=
 S四边形ODCE-S△CDE
S四边形ODCE-S△CDE=
 S△OAB+
S△OAB+ S△CAB-S△CDE
S△CAB-S△CDE=
 ×
× ×2×2+
×2×2+ ×4S△CDE-S△CDE
×4S△CDE-S△CDE=1+S△CDE,
∴S△ODE-S△CDE=1.
分析:(1)根据垂径定理由OD⊥BC得BD=
 ,在Rt△BOD中利用勾股定理即可求出OD的长;
,在Rt△BOD中利用勾股定理即可求出OD的长;(2)连接AB,根据等腰直角三角形的性质可得出AB=2
 ,再根据垂径定理得到OD⊥BC,OE⊥AC,则DE为△CBA的中位线,然后根据三角形中位线性质即可得到DE=
,再根据垂径定理得到OD⊥BC,OE⊥AC,则DE为△CBA的中位线,然后根据三角形中位线性质即可得到DE= ;
;(3)连结OC,由DE∥BA可判断△CDE∽△CBA,根据相似三角形的性质得S△CDE:S△CBA=(CD:CB)2=1:4,即S△CBA=4S△CDE,再利用S△ODB=S△ODC,S△OAE=S△OEC和S△ODE=S四边形ODCE-S△CDE进行变形可得到S△ODE-S△CDE的值.
点评:本题考查了圆的综合题:熟练掌握垂径定理;学会运用勾股定理和相似比进行几何计算;同时理解等腰直角三角形的性质.

练习册系列答案
相关题目

 如图,在一块四边形场地的四个角修建四个半径为2米的扇花台,那么四个花台的总面积是
如图,在一块四边形场地的四个角修建四个半径为2米的扇花台,那么四个花台的总面积是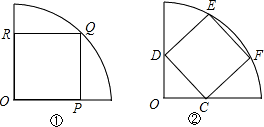

 如图,在一块四边形场地的四个角修建四个半径为2米的扇花台,那么四个花台的总面积是________平方米(结果中保留π).
如图,在一块四边形场地的四个角修建四个半径为2米的扇花台,那么四个花台的总面积是________平方米(结果中保留π).