题目内容
 如图,直线l与x轴交于点P(1,0),与x轴所夹的锐角为θ,且tanθ=
如图,直线l与x轴交于点P(1,0),与x轴所夹的锐角为θ,且tanθ= ,直线l与抛物线
,直线l与抛物线 (a>0)相交于B(m,-3),D(3,n)
(a>0)相交于B(m,-3),D(3,n)
(1)求B、D两点的坐标,并用含a的代数式表示b和c;
(2)①若关于x的方程 有实数根,求此时抛物线的解析式;
有实数根,求此时抛物线的解析式;
②若抛物线 (a>0)与x轴交于A、C两点,顺次连接A、B、C、D得凸四边形ABCD,问四边形ABCD的面积有无最大值或最小值?若有,求出面积的最大值或最小值;若无,请说明理由.
(a>0)与x轴交于A、C两点,顺次连接A、B、C、D得凸四边形ABCD,问四边形ABCD的面积有无最大值或最小值?若有,求出面积的最大值或最小值;若无,请说明理由.
解:(1)作DE⊥x轴于E,BF⊥x轴于F,如图,
∵点P(1,0),tanθ= ,D(3,n),
,D(3,n),
∴OP=1,OE=3,
∴PE=2,
在Rt△PDE中,tanθ=tan∠DPE=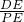 =
= ,
,
∴DE=3,
∴D点坐标为(3,3);
∵B点坐标(m,-3),
∴BF=3,
在Rt△PBF中,tanθ=tan∠FPB= =
= ,
,
∴PF=2,
∴OF=1,
∴B点坐标为(-1,-3);
把B(-1,-3)、D(3,3)代入 得
得
 ,
,
解得b= -
- ,c=-
,c=- -
- ;
;
(2)①根据题意得△=( a)2-4(a2-
a)2-4(a2- a+
a+ )≥0,
)≥0,
∴(a-1)2≤0,
∴a-1=0,即a=1,
∴此时抛物线的解析式为y=x2- x-
x- ;
;
②四边形ABCD的面积无最大值和最小值.理由如下:
AC= =a
=a =
= ,
,
∵b= -
- ,c=-
,c=- -
- ,
,
∴AC= =
=
 ,
,
∵S四边形ABCD=S△ABC+S△ADC= AC×3+
AC×3+ AC×3=3AC,
AC×3=3AC,
∴S四边形ABCD=
 ,
,
∵a>0,
∴9a2+64没有最大值,也没有最小值,即 ,没有最大值,也没有最小值
,没有最大值,也没有最小值
∴四边形ABCD的面积无最大值和最小值.
分析:(1)作DE⊥x轴于E,BF⊥x轴于F,在Rt△PDE中,利用正切的定义得到tanθ=tan∠DPE=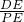 =
= ,可求出DE=3,于是确定D点坐标为(3,3);在Rt△PBF中用同样方法可确定B点坐标为(-1,-3);再把B(-1,-3)、D(3,3)代入
,可求出DE=3,于是确定D点坐标为(3,3);在Rt△PBF中用同样方法可确定B点坐标为(-1,-3);再把B(-1,-3)、D(3,3)代入 得方程组
得方程组 ,把它看作为关于b、c的方程组,解得b=
,把它看作为关于b、c的方程组,解得b= -
- ,c=-
,c=- -
- ;
;
(2)①根据根的判别式得到△=( a)2-4(a2-
a)2-4(a2- a+
a+ )≥0,整理后得到(a-1)2≤0,根据非负数的性质得到a-1=0,即a=1,即可得到此时抛物线的解析式为y=x2-
)≥0,整理后得到(a-1)2≤0,根据非负数的性质得到a-1=0,即a=1,即可得到此时抛物线的解析式为y=x2- x-
x- ;
;
②利用抛物线与x轴两交点的距离公式得到AC= =a
=a =
= ,把b=
,把b= -
- ,c=-
,c=- -
- 代入整理得到AC=
代入整理得到AC=
 ,而S四边形ABCD=S△ABC+S△ADC=
,而S四边形ABCD=S△ABC+S△ADC= AC×3+
AC×3+ AC×3=3AC,则S四边形ABCD=
AC×3=3AC,则S四边形ABCD=
 ,由于a>0,9a2+64没有最大值,也没有最小值,即
,由于a>0,9a2+64没有最大值,也没有最小值,即 ,没有最大值,也没有最小值.
,没有最大值,也没有最小值.
点评:本题考查了二次函数综合题:二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象为抛物线,其顶点式为y=a(x- )2+
)2+ ,当a>0,y最小值=
,当a>0,y最小值= ;当a<0,y最,大值=
;当a<0,y最,大值= ;对于一元二次方程的根的判别式和三角函数的定义要熟练运用.
;对于一元二次方程的根的判别式和三角函数的定义要熟练运用.

∵点P(1,0),tanθ=
 ,D(3,n),
,D(3,n),∴OP=1,OE=3,
∴PE=2,
在Rt△PDE中,tanθ=tan∠DPE=
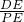 =
= ,
,∴DE=3,
∴D点坐标为(3,3);
∵B点坐标(m,-3),
∴BF=3,
在Rt△PBF中,tanθ=tan∠FPB=
 =
= ,
,∴PF=2,
∴OF=1,
∴B点坐标为(-1,-3);
把B(-1,-3)、D(3,3)代入
 得
得 ,
,解得b=
 -
- ,c=-
,c=- -
- ;
;(2)①根据题意得△=(
 a)2-4(a2-
a)2-4(a2- a+
a+ )≥0,
)≥0,∴(a-1)2≤0,
∴a-1=0,即a=1,
∴此时抛物线的解析式为y=x2-
 x-
x- ;
;②四边形ABCD的面积无最大值和最小值.理由如下:
AC=
 =a
=a =
= ,
,∵b=
 -
- ,c=-
,c=- -
- ,
,∴AC=
 =
=
 ,
,∵S四边形ABCD=S△ABC+S△ADC=
 AC×3+
AC×3+ AC×3=3AC,
AC×3=3AC,∴S四边形ABCD=

 ,
,∵a>0,
∴9a2+64没有最大值,也没有最小值,即
 ,没有最大值,也没有最小值
,没有最大值,也没有最小值∴四边形ABCD的面积无最大值和最小值.
分析:(1)作DE⊥x轴于E,BF⊥x轴于F,在Rt△PDE中,利用正切的定义得到tanθ=tan∠DPE=
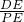 =
= ,可求出DE=3,于是确定D点坐标为(3,3);在Rt△PBF中用同样方法可确定B点坐标为(-1,-3);再把B(-1,-3)、D(3,3)代入
,可求出DE=3,于是确定D点坐标为(3,3);在Rt△PBF中用同样方法可确定B点坐标为(-1,-3);再把B(-1,-3)、D(3,3)代入 得方程组
得方程组 ,把它看作为关于b、c的方程组,解得b=
,把它看作为关于b、c的方程组,解得b= -
- ,c=-
,c=- -
- ;
;(2)①根据根的判别式得到△=(
 a)2-4(a2-
a)2-4(a2- a+
a+ )≥0,整理后得到(a-1)2≤0,根据非负数的性质得到a-1=0,即a=1,即可得到此时抛物线的解析式为y=x2-
)≥0,整理后得到(a-1)2≤0,根据非负数的性质得到a-1=0,即a=1,即可得到此时抛物线的解析式为y=x2- x-
x- ;
;②利用抛物线与x轴两交点的距离公式得到AC=
 =a
=a =
= ,把b=
,把b= -
- ,c=-
,c=- -
- 代入整理得到AC=
代入整理得到AC=
 ,而S四边形ABCD=S△ABC+S△ADC=
,而S四边形ABCD=S△ABC+S△ADC= AC×3+
AC×3+ AC×3=3AC,则S四边形ABCD=
AC×3=3AC,则S四边形ABCD=
 ,由于a>0,9a2+64没有最大值,也没有最小值,即
,由于a>0,9a2+64没有最大值,也没有最小值,即 ,没有最大值,也没有最小值.
,没有最大值,也没有最小值.点评:本题考查了二次函数综合题:二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象为抛物线,其顶点式为y=a(x-
 )2+
)2+ ,当a>0,y最小值=
,当a>0,y最小值= ;当a<0,y最,大值=
;当a<0,y最,大值= ;对于一元二次方程的根的判别式和三角函数的定义要熟练运用.
;对于一元二次方程的根的判别式和三角函数的定义要熟练运用. 
练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
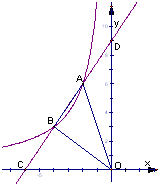 如图,直线AB与x轴交于点C,与反比例函数
如图,直线AB与x轴交于点C,与反比例函数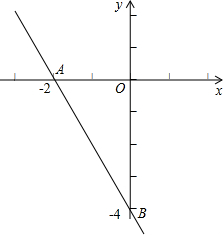 如图,直线AB与x轴交于点A,与y轴交于点B.
如图,直线AB与x轴交于点A,与y轴交于点B. 已知:如图,直线AB与x轴交于点A,与y轴交于点B.
已知:如图,直线AB与x轴交于点A,与y轴交于点B. 所示.
所示. (2012•聊城)如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(2012•聊城)如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).