题目内容
【题目】如图①,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=40°,连接BD、CE.将△ADE绕点A旋转,BD、CE也随之运动.
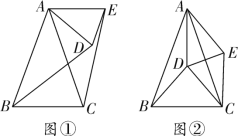
(1)求证:BD=CE;
(2)在△ADE绕点A旋转过程中,当AE∥BC时,求∠DAC的度数;
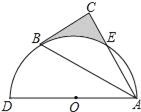
(3)如图②,当点D恰好是△ABC的外心时,连接DC,判断四边形ADCE的形状,并说明理由.
【答案】(1)见详解;(2)![]() ;(3)四边形ADCE是菱形.
;(3)四边形ADCE是菱形.
【解析】
(1)利用SAS证明![]() 由全等三角形对应角相等的性质可得结论;
由全等三角形对应角相等的性质可得结论;
(2)由等腰三角形两底角相等及三角形内角和定理可知![]() 的度数,由两直线平行,同旁内角互补可知
的度数,由两直线平行,同旁内角互补可知![]() 的度数,易求∠DAC的度数;
的度数,易求∠DAC的度数;
(3)利用利用SAS证明![]() 可得
可得![]() ,由点D是△ABC的外心可得
,由点D是△ABC的外心可得![]() ,由四条边都相等的四边形是菱形可判定四边形ADCE的形状.
,由四条边都相等的四边形是菱形可判定四边形ADCE的形状.
解:(1)![]()
![]()
![]()
在![]() 和
和![]() 中
中
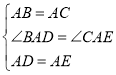
![]()
![]()
(2)![]()
![]()
![]()
![]()
![]()
![]() ;
;
(3)![]()
![]()
![]()
在![]() 和
和![]() 中
中
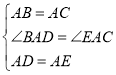
![]()
![]()
![]() 点D是△ABC的外心,即点D为三角形三边垂直平分线的交点
点D是△ABC的外心,即点D为三角形三边垂直平分线的交点
![]()
![]()
所以四边形ADCE是菱形.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目