题目内容
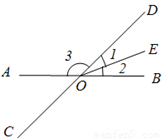
 已知直线l⊥n于点O,作直线AB交这两条直线于点A、B.若OA=2,OB=mOA,且三角形OAB的面积为6,如图是其中的一种情形,则符合条件的直线AB最多可作
已知直线l⊥n于点O,作直线AB交这两条直线于点A、B.若OA=2,OB=mOA,且三角形OAB的面积为6,如图是其中的一种情形,则符合条件的直线AB最多可作8
8
条.分析:根据条件求得点A、B的坐标,然后由两点确定一条直线写出符合条件的直线AB.
解答:解:∵OA=2,OB=mOA,
∴OB=2m
又∵三角形OAB的面积为6,
∴
×2×2m=6,
即m=3.
∴OB=6.
∴点A1(2,0)、A2(-2,0)、A3(0,2)、A4(0,2)与点B1(0,6)、B2(0,-6)、B3(6,-0)、B4(-6,0)都符合题意,
∴符合条件的直线有:直线A1B1,直线A1B2,直线A2B1,直线A2B1,直线A3B3,直线A2B3,直线A3B4,直线A4B4,共有8条.
故答案是:8.
∴OB=2m
又∵三角形OAB的面积为6,
∴
| 1 |
| 2 |
即m=3.
∴OB=6.
∴点A1(2,0)、A2(-2,0)、A3(0,2)、A4(0,2)与点B1(0,6)、B2(0,-6)、B3(6,-0)、B4(-6,0)都符合题意,
∴符合条件的直线有:直线A1B1,直线A1B2,直线A2B1,直线A2B1,直线A3B3,直线A2B3,直线A3B4,直线A4B4,共有8条.
故答案是:8.
点评:本题考查了三角形的面积.解答此题时,一定要找全符合条件的点A、B的坐标.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
 4、如图,已知直线PQ⊥MN于点O,点A,B分别在MN,PQ上,OA=1,OB=2,在直线MN或直线PQ上找一点C,使△ABC是等腰三角形,则这样的C点有( )
4、如图,已知直线PQ⊥MN于点O,点A,B分别在MN,PQ上,OA=1,OB=2,在直线MN或直线PQ上找一点C,使△ABC是等腰三角形,则这样的C点有( )
 、
、 交于点
交于点 ,
,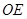 平分
平分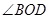 ,若
,若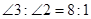 ,
,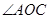 的度数.
的度数.