题目内容
若线段AB=4cm,点C是线段AB的黄金分割点,AC>BC,求AC-BC的值.
考点:黄金分割
专题:
分析:根据黄金分割的定义分别表示出AC和BC的长,再求出AC-BC的值即可.
解答:解:∵点C是线段AB的黄金分割点,AC>BC,
∴AC=
AB=
×4=2
-2,
∴BC=4-AC=6-2
,
∴AC-BC=2
-2-6+2
=4
-8.
∴AC=
| ||
| 2 |
| ||
| 2 |
| 5 |
∴BC=4-AC=6-2
| 5 |
∴AC-BC=2
| 5 |
| 5 |
| 5 |
点评:考查了黄金分割点的概念,熟悉黄金分割的比值是本题的关键,把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值是
.
| ||
| 2 |

练习册系列答案
相关题目
下列方程是一元二次方程的是( )
A、
| ||
| B、x2+2x-y=3 | ||
| C、ax2-bx=5(a和b为常数) | ||
| D、m2-2m=3 |
计算-5+6的结果是( )
| A、-1 | B、1 | C、-5 | D、-6 |
在同圆中,若AB和CD都是劣弧,且AB=2CD,那么弦AB和CD的大小关系是( )
| A、AB=2CD |
| B、AB>2CD |
| C、AB<2CD |
| D、无法比较它们的大小 |
一个多边形除去一内角外,其余各内角之和为1688°,则除去的这个内角的度数为( )
| A、68° | B、102° |
| C、78° | D、112° |
 如图所示,AB=AC,∠B=∠C,点D、E分别在AB、AC上,且点F是DE的中点,求证:AF⊥DE.
如图所示,AB=AC,∠B=∠C,点D、E分别在AB、AC上,且点F是DE的中点,求证:AF⊥DE.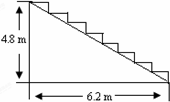 遂昌元立大酒店在重新装修后,准备在大厅的主梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼道宽2m,其侧面如图所示,则购买地毯至少需要
遂昌元立大酒店在重新装修后,准备在大厅的主梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼道宽2m,其侧面如图所示,则购买地毯至少需要