如图.已知AB=AC.∠A=440.AB的垂直平分线MN交AC于点D.则∠DBC= . 题目和参考答案——青夏教育精英家教网—

题目内容

如图，已知AB=AC，∠A=440，AB的垂直平分线MN交AC于点D，则∠DBC= 。

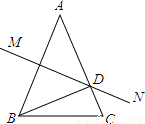
24°．

【解析】

试题分析：根据等腰三角形两底角相等求出∠ABC，再根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD，根据等边对等角求出∠ABD，然后求解即可．

试题解析：∵AB=AC，∠A=44°，

∴∠ABC=（180°-∠A）=×（180°-44°）=68°，

∵MN是AB的垂直平分线，

∴AD=BD，

∴∠ABD=∠A=44°，

∴∠DBC=∠ABC-∠ABD=68°-44°=24°．

考点：1．线段垂直平分线的性质；2．等腰三角形的性质．

练习册系列答案

相关题目

如图，△ABC的顶点A、B、C均在⊙O上，若∠ABC+∠AOC=90°，则∠AOC的大小是（）

A．30° B．45° C．60° D．70°

对于抛物线y=－（x＋1）2＋3，下列结论：①抛物线的开口向下；②对称轴为直线x=1；③顶点坐标为（－1，3）；④x＞1时，y随x的增大而减小，

其中正确结论的个数为（）

A．1 B．2 C．3 D．4

如图，在Rt△ABC中，∠C=90°，AC=8cm，BC=6CM．点P，Q同时由B，A两点出发，分别沿射线BC，AC方向以1cm/s的速度匀速运动．

（1）几秒后△PCQ的面积是△ABC面积的一半？

（2）连结BQ，几秒后△BPQ是等腰三角形？

如图，圆柱形玻璃杯高为12cm、底面周长为18cm，在杯内离杯底4cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离为 cm．

三角形两边长为6和8，第三边是方程x2-16x+60=0的根，则该三角形的面积是（）

A．24 B．24或8 C．48 D．8

如图，△ABC中，∠B，∠C的角平分线相交于点O，过O作DE∥BC，若BD+CE=5，则DE等于（）

A．7 B．6 C．5 D．4

把x2y﹣2y2x+y3分解因式为 .

“龟兔首次赛跑”之后，输了比赛的兔子没有气馁，总结反思后，和乌龟约定再赛一场．图中的函数图象刻画了“龟兔再次赛跑”的故事（表示乌龟从起点出发所行的时间，表示乌龟所行的路程，表示兔子所行的路程）．有下列说法：①“龟兔再次赛跑”的路程为1000米；②兔子和乌龟同时从起点出发；③乌龟在途中休息了10分钟；④兔子在途中750米处追上乌龟．其中正确的说法是．（把你认为正确说法的序号都填上）

试题分类