题目内容
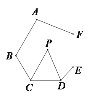
【题目】如图,在六边形ABCDEF中,∠A+∠B+∠E+∠F=α,CP、DP分别平分∠BCD、∠CDE,则∠P的度数是( )
A. ![]() α-180°B. 180°-
α-180°B. 180°-![]() C.
C. ![]() D. 360°-
D. 360°-![]()
【答案】A
【解析】
根据六边形的内角和公式表示出∠EDC+∠BCD,然后根据角平分线的定义可得∠PDC=![]() ∠EDC,∠PCD=
∠EDC,∠PCD=![]() ∠BCD,然后根据三角形内角和定理列式整理即可得解.
∠BCD,然后根据三角形内角和定理列式整理即可得解.
解:六边形ABCDEF的内角和为:(6-2)180°=720°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠PDC=![]() ∠EDC,∠PCD=
∠EDC,∠PCD=![]() ∠BCD,
∠BCD,
∴∠P=180°-∠PDC-∠PCD
=180°-![]() ∠EDC-
∠EDC-![]() ∠BCD
∠BCD
=180°-![]() (∠EDC+∠BCD)
(∠EDC+∠BCD)
=180°-![]() (720°-∠A-∠B-∠E-∠F)
(720°-∠A-∠B-∠E-∠F)
=![]() (∠A+∠B+∠E+∠F)-180°,
(∠A+∠B+∠E+∠F)-180°,
即∠P=![]() (∠A+∠B+∠E+∠F)-180°.又∵∠A+∠B+∠E+∠F=α,
(∠A+∠B+∠E+∠F)-180°.又∵∠A+∠B+∠E+∠F=α,
故答案为:∠P=![]() α-180°.
α-180°.
故选:A.

练习册系列答案
相关题目