题目内容
如图，点A的坐标是（2，2），若点P在x轴上，且△APO是等腰三角形，则点P的坐标不可能是（ ）
A．（4，0）
B．（1，0）
C．（-2
，0）D．（2，0）
【答案】分析：本题要可先根据两点的距离公式求出OA的长，再根据选项的P点的坐标分别代入，求出OP、AP的长，根据三角形的判别公式化简即可得出P点坐标的不可能值．
解答：
解：点A的坐标是（2，2），
根据勾股定理：则OA=2
，
若点P的坐标是（4，0），则OP=4，过A作AC⊥X轴于C，
在直角△ACP中利用勾股定理，就可以求出AP=2
，∴AP=OA，
同理可以判断（1，0），（-2
，0），（2，0）是否能构成等腰三角形，
经检验点P的坐标不可能是（1，0）．
故选B．
点评：已知点的坐标可以转化为利用勾股定理求线段的长的问题．
解答：
解：点A的坐标是（2，2），根据勾股定理：则OA=2
，若点P的坐标是（4，0），则OP=4，过A作AC⊥X轴于C，
在直角△ACP中利用勾股定理，就可以求出AP=2
，∴AP=OA，同理可以判断（1，0），（-2
，0），（2，0）是否能构成等腰三角形，经检验点P的坐标不可能是（1，0）．
故选B．
点评：已知点的坐标可以转化为利用勾股定理求线段的长的问题．
练习册系列答案
相关题目
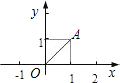如图，点A的坐标是（1，1），若点B在x轴上，且△ABO是等腰三角形，则点B的坐标不可能是（ ）| A、（2，0） | ||
B、（
| ||
C、（-
| ||
| D、（1，0） |
15、如图，点P的坐标是（ ）
（2013•济南）如图，点A的坐标是（-2，0），点B的坐标是（6，0），点C在第一象限内且△OBC为等边三角形，直线BC交y轴于点D，过点A作直线AE⊥BD，垂足为E，交OC于点F．
（2012•槐荫区二模）如图，点B的坐标是（4，4），作BA⊥x轴于点A，作BC⊥y轴于点C，反比例函数
（2012•甘井子区模拟）如图，点A的坐标是（ ）