题目内容

定理1　（塞瓦（Ceva）定理）：
设P，Q，R分别是△ABC的BC，CA，AB边上的点．若AP，BQ，CR相交于一点M，则 $数学公式$ ．

证明：如图，由三角形面积的性质，有
$\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
以上三式相乘，得 $\text{[math]}$ ．
分析：先作出图形，再根据三角形面积的性质可知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，三式相乘即可得到题干结论．
点评：本题主要考查三角形的面积的知识点，根据比例求出三角形的面积是解答此题的关键．

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

一个角的平分线的尺规作法，其理论依据是全等三角形判定定理（　　）

定理1 （塞瓦（Ceva）定理）：
设P，Q，R分别是△ABC的BC，CA，AB边上的点．若AP，BQ，CR相交于一点M，则

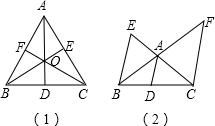利用塞瓦定理可以简便地证明重心定理、内心定理和垂心定理：

AM是△ABC的中线，O为AM上任一点，BO交AC于F，CO交AB于E，试用塞瓦定理证明EF∥BC．