题目内容
18. 如图,在直角△ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于点D,这时∠BDC的度数是105°.
如图,在直角△ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于点D,这时∠BDC的度数是105°.
分析 由旋转的性质得:BC=B′C,∠B′=∠ABC=55°,∠A′=∠A=35°,由等腰三角形的性质得到∠B′BC=∠B′=55°,进而求得∠A′BD,根据三角形外角定理即可得出∠BDC的度数.
解答 解:∠ABC=90°-∠A=55°
由旋转的性质得:BC=B′C,∠B′=∠ABC=55°,∠A′=∠A=35°,
∴∠B′BC=∠B′=55°,
∴∠A′BD=180°-55°-55°=70°,
∴∠BDC=∠A′+∠A′BD=105°,
故答案为:105°.
点评 本题考查了旋转的性质、等腰三角形的判定与性质、三角形外角定理;熟练掌握旋转的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
8.对于事件“从车间生产的100个(其中有2个是次品)产品中任意抽一个,所抽取的产品是次品”,下列对于该事件的描述正确的是( )
| A. | 该事件是必然事件 | B. | 该事件是不可能事件 | ||
| C. | 该事件是不确定事件 | D. | 该事件发生的可能性很大 |
6.如图,在长为a厘米的木条上钻4个圆孔,每个圆孔的直径为2厘米,则x等于( )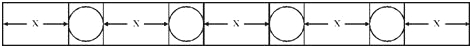
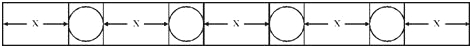
| A. | $\frac{a-8}{5}$厘米 | B. | $\frac{a+8}{5}$厘米 | C. | $\frac{a-4}{5}$厘米 | D. | $\frac{a-16}{5}$厘米 |
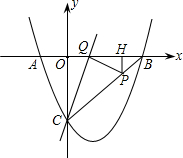 如图,已知抛物线y=$\frac{3}{4}{x}^{2}$+bx+c与轴交于A、B两点,与y轴交于C点,A的坐标为(-1,0),过点C的直线y=$\frac{3}{4t}$x-3与x轴交于点Q,点P是线段BC上的动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
如图,已知抛物线y=$\frac{3}{4}{x}^{2}$+bx+c与轴交于A、B两点,与y轴交于C点,A的坐标为(-1,0),过点C的直线y=$\frac{3}{4t}$x-3与x轴交于点Q,点P是线段BC上的动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1. 如图,△ABC平移得到△DEF,并且DE由线段AB平移而得,AB=BC=4cm,DF=5cm.则△DEF的周长是13cm.
如图,△ABC平移得到△DEF,并且DE由线段AB平移而得,AB=BC=4cm,DF=5cm.则△DEF的周长是13cm.