题目内容
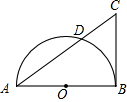如图，AB是半圆O的直径，CB是半圆O的切线，B是切点，AC交半圆O于点D．已知CD=1，AD=3，那么cos∠CAB=________．
分析：根据切割线定理可知CB2=CD•CA=4，先求得CD=2；结合Rt△CAB中的条件可求得AB=2
，即可求得cos∠CAB=
=．解答：∵CB2=CD•CA=4，
∴CB=2．
在Rt△CAB中，CB=2，CA=4，
∴AB=2
．∴cos∠CAB=
=．点评：本题考查切割线定理和锐角三角函数的定义：在直角三角形中，正弦等于对边比斜边；余弦等于邻边比斜边；正切等于对边比邻边．
练习册系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
如图，AB是半圆O的直径，AC是弦，点P从点B开始沿BA边向点A以1cm/s的速度移动，若AB长为10cm，点O到AC的距离为4cm．
已知：如图，AB是半圆O的直径，OD是半径，BM切半圆于点B，OC与弦AD平行交BM于点C．
如图，AB是半圆O的直径，点D是半圆上一动点，AB=10，AC=8，当△ACD是等腰三角形时，点D到AB的距离是
如图，AB是半圆O的直径，以OA为直径的半圆O′与弦AC交于点D，O′E∥AC，并交OC于点E，则下列结论：①S△O′OE=
