题目内容
直线y=x+1与x轴、y轴分别交于A、B两点,点C在坐标轴上,若△ABC为等腰三角形,则满足条件的点C最多有________ 个.
7
分析:由直线y=x+1的方程,分别令y=0,x=0求出直线与x轴,y轴的交点A与B的坐标,然后分三种情况考虑:当AB为底边时,显然C与原点重合,此时三角形ABC为等腰三角形;当AB为腰,A为顶点时,以A为圆心,AB长为半径画弧,与坐标轴交于3点,可得出C的位置有3处;当AB为腰,B为顶点时,以B为圆心,AB长为半径画弧,与坐标轴交于3点,同理可得C位置也有3处,综上,得到满足条件C的总个数.
解答:令直线y=x+1中,y=0,解得x=-1,直线y=x+1与x轴的交点为A(-1,0),
令x=0,解得y=1,直线y=x+1与y轴的交点为B(0,1),
分三种情况考虑:
①以AB为底,C在原点;
②以AB为腰,且A为顶点,C点有3种可能位置;
③以AB为腰,且B为顶点,C点有3种可能位置,
则满足条件的点C最多有7个.
故答案为:7
点评:本题考查了一次函数的综合应用,对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.
分析:由直线y=x+1的方程,分别令y=0,x=0求出直线与x轴,y轴的交点A与B的坐标,然后分三种情况考虑:当AB为底边时,显然C与原点重合,此时三角形ABC为等腰三角形;当AB为腰,A为顶点时,以A为圆心,AB长为半径画弧,与坐标轴交于3点,可得出C的位置有3处;当AB为腰,B为顶点时,以B为圆心,AB长为半径画弧,与坐标轴交于3点,同理可得C位置也有3处,综上,得到满足条件C的总个数.
解答:令直线y=x+1中,y=0,解得x=-1,直线y=x+1与x轴的交点为A(-1,0),
令x=0,解得y=1,直线y=x+1与y轴的交点为B(0,1),
分三种情况考虑:
①以AB为底,C在原点;
②以AB为腰,且A为顶点,C点有3种可能位置;
③以AB为腰,且B为顶点,C点有3种可能位置,
则满足条件的点C最多有7个.
故答案为:7
点评:本题考查了一次函数的综合应用,对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•兰州)如图,M为双曲线y=
(2012•兰州)如图,M为双曲线y=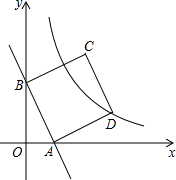 (2013•宛城区一模)如图,直线y=-2x+2与x轴y轴分别相交于点A、B,四边形ABCD是正方形,曲线y=
(2013•宛城区一模)如图,直线y=-2x+2与x轴y轴分别相交于点A、B,四边形ABCD是正方形,曲线y=