Question

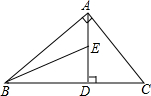如图，△ABC中，∠BAC=90°，AD⊥BC于D，E是AD上一点，下列说法正确的是

1. A.
   ∠BED＞∠C
2. B.
   ∠BED=∠C
3. C.
   ∠BED＜∠C
4. D.
   不一定

Answer 1

A
分析：根据三角形的一个外角大于任何一个与它不相邻的内角可得∠BED＞∠BAD，再根据同角的余角相等求出∠BAD=∠C，然后解答即可．
解答：∵∠BED是△ABE的外角，
∴∠BED＞∠BAD，
△ABC中，∠BAC=90°，AD⊥BC于D，
∴∠BAD=∠C，
∴∠BED＞∠C．
故选A．
点评：本题考查了三角形的外角性质，熟记三角形的一个外角大于任何一个与它不相邻的内角是解题的关键．