Question

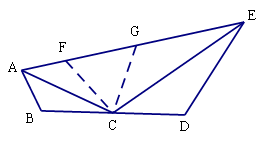
在四边形ABDE中，C是BD边的中点．

（1）如图(1)，若AC平分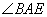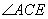，=90°, 则线段AE、AB、DE的长度满足的数量关系为

                        ；（直接写出答案）

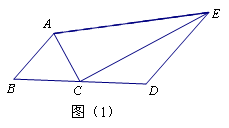
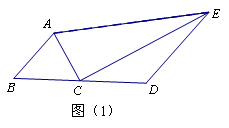
（2）如图（2），AC平分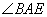， EC平分，

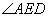若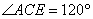，则线段AB、BD、DE、AE的长度满足怎样的数量关系？写出结论并证明；

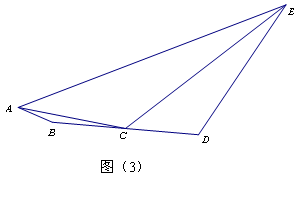
（3）如图（3），BD = 8，AB=2，DE=8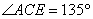，，则线段AE长度的最大值是____________（直接写出答案）．

Answer 1

（1） AE=AB+DE ；

（2）解：猜想：AE=AB+DE+．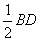

证明：在AE上取点F，使AF=AB，连结CF，

在AE上取点G，使EG=ED，连结CG．

∵C是BD边的中点，∴CB=CD=．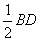

∵AC平分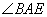，∴∠BAC=∠FAC．

∵AF=AB，AC=AC，∴△ABC≌△AFC.

∴CF=CB，∴∠BCA=∠FCA．同理可证：CD=CG，∴∠DCE=∠GCE．

∵CB=CD，∴CG=CF

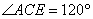∵，∴∠BCA+∠DCE=180°-120°=60°．                   图（2）

∴∠FCA+∠GCE=60°．∴∠FCG=60°．

∴△FGC是等边三角形．∴FG=FC=．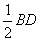

∵AE=AF+EG+FG．

∴AE=AB+DE+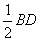．（3）．