题目内容
10.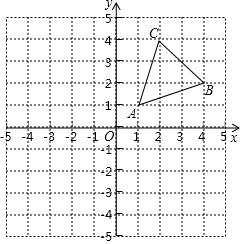 已知,在如图所示的网格中建立平面直角坐标系后,△ABC三个頂点的坐标分别为A(1,1),B(4,2),C(2,4).
已知,在如图所示的网格中建立平面直角坐标系后,△ABC三个頂点的坐标分别为A(1,1),B(4,2),C(2,4).(1)画出△ABC关于y轴对称的△A1B1C1;
(2)借助图中的网格,请只用直尺(不含刻度)完成以下要求:(友情提醒:请别忘了标注宇母)
①在图中找一点P,使得P到AB、AC的距离相等,且PA=PB;
②在x轴上找一点Q,使得△QAB的周长最小,并求此时点Q的坐标.
分析 (1)画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始,连接这些对称点,就得到原图形的轴对称图形;
(2)①作∠BAC的角平分线,作AB的垂直平分线,交于点P,则点P即为所求;②作点B关于x轴对称的点B',连接AB',交x轴于Q,则点Q即为所求.根据直线AB'的解析式即可得出点Q的坐标.
解答 解:(1)如图所示,△A1B1C1即为所求;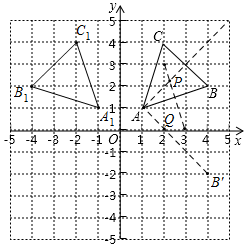
(2)①如图所示,作∠BAC的角平分线,作AB的垂直平分线,交于点P,则点P即为所求;
②如图所示,作点B关于x轴对称的点B',连接AB',交x轴于Q,则点Q即为所求,
∵A(1,1),B'(4,-2),
∴可设直线AB'为y=kx+b,则
$\left\{\begin{array}{l}{1=k+b}\\{-2=4k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=2}\end{array}\right.$,
∴y=-x+2,
当y=0时,-x+2=0,
解得x=2,
此时点Q的坐标为(2,0).
点评 本题主要考查了利用轴对称进行作图,解决问题的关键是掌握角平分线的性质,中垂线的性质以及待定系数法求一次函数解析式,解题时注意:两点之间,线段最短.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.算式[(-8)-□]÷(-2)=4中,□表示的数是( )
| A. | 1 | B. | -1 | C. | -2 | D. | 0 |
1.(1.2计算3.4分解因式)
(1)($\sqrt{2}$+1)0-(-$\frac{1}{2}$)2+2-2
(2)(2a-3b)(-3b-2a)
(3)3m2-24m+48
(4)x3y-4xy.
(1)($\sqrt{2}$+1)0-(-$\frac{1}{2}$)2+2-2
(2)(2a-3b)(-3b-2a)
(3)3m2-24m+48
(4)x3y-4xy.
19.下列二次根式中是最简二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{\frac{3}{2}}$ | C. | $\sqrt{6}$ | D. | $\sqrt{0.01}$ |
20.下列事件中属于随机事件的是( )
| A. | 抛掷一石头,石头终将落地 | B. | 从装有黑球,白球的袋里摸出红球 | ||
| C. | 太阳绕着地球转 | D. | 买1张彩票,中500万大奖 |
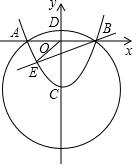 如图,抛物线y=ax2-4与x轴相交于A(-3,0)、B,与y轴相交于点C.以点C为圆心,CA长为半径画⊙C,⊙C与y轴的正半轴相交于点D.
如图,抛物线y=ax2-4与x轴相交于A(-3,0)、B,与y轴相交于点C.以点C为圆心,CA长为半径画⊙C,⊙C与y轴的正半轴相交于点D. 如图,AB与DE相交于点O,OC⊥AB,OF是∠AOE的角平分线,若∠COD=36°,则∠AOF=27°.
如图,AB与DE相交于点O,OC⊥AB,OF是∠AOE的角平分线,若∠COD=36°,则∠AOF=27°.