题目内容
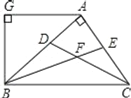
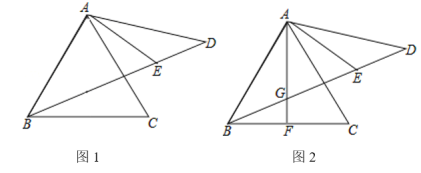
【题目】如图1,D是等边△ABC外一点,且AD=AC,连接BD,∠CAD的角平分交BD于E.
(1)求证:∠ABD=∠D;
(2)求∠AEB的度数;
(3)△ABC 的中线AF交BD于G(如图2),若BG=DE,求![]() 的值.
的值.
【答案】(1)见解析;(2)60°;(3)![]()
【解析】
(1)利用等边三角形的性质可得AB=AC,又因为AD=AC已知,所以AB=AD,进而得到本题答案;
(2) 设∠3=∠D=x°,∠1=∠2=y°,利用等边三角形的性质以及三角形内角和定理得出∠3+∠D+∠BAD=180°,进而得出答案;
(3)首先得出△ABE≌△ADG ,进而得出∠4=∠AEB=60°,进而求出DE=BG=2GF, AG= BG=2GF, AF=AG+GF=3FG,即可得出答案.
解:(1)∵AB=AC,AD=AC,
∴AB=AD,
∴∠3=∠D(即∠ABD=∠D)
(2)∵AE平分∠CAD,
∴∠1=∠2,
∵△ABC是等边三角形,
∴∠BAC=60°,
设∠3=∠D=x°,∠1=∠2=y°,
∵∠3+∠D+∠BAD=180°,
∴x +x + 60° +2y =180°,
∴x +y =60°,
∴∠AEB=∠1+∠D = x +y = 60°;
(3)∵BG=DE,
∴BE=DG,
在△ABE和△ADG中,
![]()
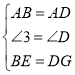 ,
,
∴△ABE≌△ADG(SAS)
∴∠4=∠AEB=60°
∵△ABC是等边三角形,F是BC中点,
∴∠AFB=90°,∠7=30°,
∵∠6=90°﹣∠5=30°,
∴DE=BG=2GF,
∵∠3=60°﹣∠6=30°=∠7,
∴AG=BG=2GF,
∴AF=AG+GF=3FG,
∴![]() .
.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目