题目内容
【题目】如图,抛物线y=﹣x2+bx+c与直线y= ![]() x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,
x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3, ![]() ).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.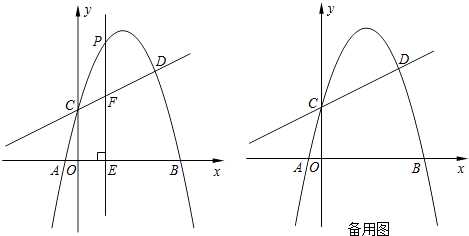
(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O、C、P、F为顶点的四边形是平行四边形?请说明理由.
(3)若存在点P,使∠PCF=45°,请直接写出相应的点P的坐标.
【答案】
(1)
解:在直线解析式y= ![]() x+2中,令x=0,得y=2,
x+2中,令x=0,得y=2,
∴C(0,2).
∵点C(0,2)、D(3, ![]() )在抛物线y=﹣x2+bx+c上,
)在抛物线y=﹣x2+bx+c上,
∴  ,
,
解得b= ![]() ,c=2,
,c=2,
∴抛物线的解析式为:y=﹣x2+ ![]() x+2.
x+2.
(2)
解:∵PF∥OC,且以O、C、P、F为顶点的四边形是平行四边形,
∴PF=OC=2,
∴将直线y= ![]() x+2沿y轴向上、下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.
x+2沿y轴向上、下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.
由答图1可以直观地看出,这样的交点有3个.
将直线y= ![]() x+2沿y轴向上平移2个单位,得到直线y=
x+2沿y轴向上平移2个单位,得到直线y= ![]() x+4,
x+4,
联立  ,
,
解得x1=1,x2=2,
∴m1=1,m2=2;
将直线y= ![]() x+2沿y轴向下平移2个单位,得到直线y=
x+2沿y轴向下平移2个单位,得到直线y= ![]() x,
x,
联立  ,
,
解得x3= ![]() ,x4=
,x4= ![]() (在y轴左侧,不合题意,舍去),
(在y轴左侧,不合题意,舍去),
∴m3= ![]() .
.
∴当m为值为1,2或 ![]() 时,以O、C、P、F为顶点的四边形是平行四边形.
时,以O、C、P、F为顶点的四边形是平行四边形.

(3)
解:存在.
理由:设点P的横坐标为m,则P(m,﹣m2+ ![]() m+2),F(m,
m+2),F(m, ![]() m+2).
m+2).
如答图2所示,过点C作CM⊥PE于点M,则CM=m,EM=2,
∴FM=yF﹣EM= ![]() m,
m,
∴tan∠CFM=2.
在Rt△CFM中,由勾股定理得:CF= ![]() m.
m.
过点P作PN⊥CD于点N,
则PN=FNtan∠PFN=FNtan∠CFM=2FN.
∵∠PCF=45°,
∴PN=CN,
而PN=2FN,
∴FN=CF= ![]() m,PN=2FN=
m,PN=2FN= ![]() m,
m,
在Rt△PFN中,由勾股定理得:PF= ![]() =
= ![]() m.
m.
∵PF=yP﹣yF=(﹣m2+ ![]() m+2)﹣(
m+2)﹣( ![]() m+2)=﹣m2+3m,
m+2)=﹣m2+3m,
∴﹣m2+3m= ![]() m,
m,
整理得:m2﹣ ![]() m=0,
m=0,
解得m=0(舍去)或m= ![]() ,
,
∴P( ![]() ,
, ![]() );
);
同理求得,另一点为P( ![]() ,
, ![]() ).
).
∴符合条件的点P的坐标为( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ).
).

【解析】(1)首先求出点C的坐标,然后利用待定系数法求出抛物线的解析式;(2)本问采用数形结合的数学思想求解.将直线y= ![]() x+2沿y轴向上或向下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.由答图1可以直观地看出,这样的交点有3个.联立解析式解方程组,即可求出m的值;(3)本问符合条件的点P有2个,如答图2所示,注意不要漏解.在求点P坐标的时候,需要充分挖掘已知条件,构造直角三角形或相似三角形,解方程求出点P的坐标.
x+2沿y轴向上或向下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.由答图1可以直观地看出,这样的交点有3个.联立解析式解方程组,即可求出m的值;(3)本问符合条件的点P有2个,如答图2所示,注意不要漏解.在求点P坐标的时候,需要充分挖掘已知条件,构造直角三角形或相似三角形,解方程求出点P的坐标.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

【题目】下表是某中学八年级的1000名学生最喜欢的球类活动统计表:
最喜欢的 球类活动 | 篮球 | 排球 | 足球 | 乒乓球 | 其他 |
人数 | 185 | 175 | 260 | 330 | 50 |
(1)哪种球类运动最受欢迎?
(2)哪两种球类运动受欢迎的程度差不多?
(3)八年级学生最喜欢的各类球类活动的频率各是多少?