Question

如图，在平面直角坐标系中，点0为坐标原点，直线交x轴于点A，交y轴于点B，BD平分∠AB0，点C是x轴的正半轴上一点，连接BC，且AC=AB．

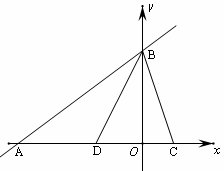
（1）求直线BD的解析式：

（2）过C作CH∥y轴交直线AB于点H，点P是射线CH上的一个动点，过点P作PE⊥CH，直线PE交直线BD于E、交直线BC于F，设线段EF的长为d(d≠0)，点P的纵坐标为t，求d与t之间的函数关系式，并写出自变量t的取值范围；

（3）在（2）的条件下，取线段AB的中点M，y轴上有一点N．试问：是否存在这样的t的值，使四边形PEMN是平行四边形，若存在，请求出t的值；若不存在，请说明理由．

Answer 1

（1）；（2）当0≤＜6时，，当＞6时，；（3）2

【解析】

试题分析：（1）先求出直线与坐标轴的交点坐标，即可求得AO、BO的长，在Rt△AOB中，根据勾股定理可以求得AB的长，过点D作DG⊥AB于点G，根据角平分线的性质可求得OD=DG，设OD=DG=，由根据三角形的面积公式即可列方程求得a的值，从而可以求得点D的坐标，设直线BD的解析式为，将B（0，6），D（-3，0）代入即可求得结果；

（2）由AC=AB=10，OA=8可求得OC的长，即可得到点C的坐标，设直线BC的解析式为，将B（0，6），C（2，0）代入即可求得直线BC的解析式，由CH//轴，点P的纵坐标为，所以当时，有或，即可表示出点E、F的坐标，再分当0≤＜6时，当＞6时两种情况分析；

（3）由点M为线段AB的中点易求得点M的坐标，即可求得MN的长，根据平行四边形的性质可得MN//PE，MN=PE=4，由（2）得：E（，），P（2，），再根据PE==4，即可求得结果.

解：（1）当时，，，当时， 

∴A（-8，0），B（0，6） 

∴AO=8，OB=6

在Rt△AOB中，，所以AB=10

过点D作DG⊥AB于点G

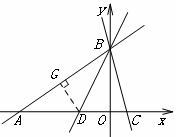
∵BD平分∠ABO，OB⊥OA   

∴OD=DG

设OD=DG=

∵

∴

即，解得  

∴D（-3，0）

设直线BD的解析式为

将B（0，6），D（-3，0）代入得：

   解得：

∴直线BD的解析式为

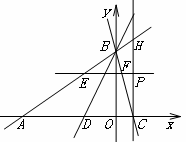
（2）∵AC=AB=10，OA=8

∴OC=10-8=2 

∴C（2，0）

设直线BC的解析式为

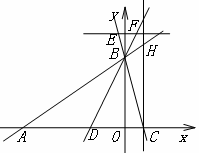
将B（0，6），C（2，0）代入

    解得：

∴直线BC的解析式为

∵CH//轴，点P的纵坐标为

∴当时，有或

∴或

∴E（，），F（，）

①当0≤＜6时，EF=，解得

②当＞6时，EF=，解得；

（3）由点M为线段AB的中点

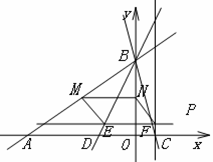
易求：M（-4，3）

∴MN=4

∵四边形PEMN是平行四边形

∴MN//PE，MN=PE=4

由（2）得：E（，），P（2，）

∴PE==4，解得=2

∴存在这样的=2，使得四边形PEMN是平行四边形.

考点：动点问题的综合题

点评：此类问题难度较大，在中考中比较常见，一般在压轴题中出现，需特别注意.