题目内容
在△ABC中,I是外心,且∠BIC=130°,则∠A的度数是
- A.65°
- B.115°
- C.65°或115°
- D.65°或130°
C
分析:由于三角形的外心的位置的不同,应分为两种情况考虑:外心在三角形的内部或外心在三角形的外部.
然后根据三角形的外心是三角形外接圆的圆心,结合一条弧所对的圆周角等于它所对的圆心角的一半进行分析求解.
解答:当三角形的外心在三角形的内部时,则∠A= ∠BIC=65°;
∠BIC=65°;
当三角形的外心在三角形的外部时,则∠A=180°- ∠BIC=115°.
∠BIC=115°.
故选C.
点评:注意:在△ABC中,I是外心,则当外心在三角形的内部时,有∠A= ∠BIC;当外心在三角形的外部时,则有∠A=180°-
∠BIC;当外心在三角形的外部时,则有∠A=180°- ∠BIC.
∠BIC.
分析:由于三角形的外心的位置的不同,应分为两种情况考虑:外心在三角形的内部或外心在三角形的外部.
然后根据三角形的外心是三角形外接圆的圆心,结合一条弧所对的圆周角等于它所对的圆心角的一半进行分析求解.
解答:当三角形的外心在三角形的内部时,则∠A=
 ∠BIC=65°;
∠BIC=65°;当三角形的外心在三角形的外部时,则∠A=180°-
 ∠BIC=115°.
∠BIC=115°.故选C.
点评:注意:在△ABC中,I是外心,则当外心在三角形的内部时,有∠A=
 ∠BIC;当外心在三角形的外部时,则有∠A=180°-
∠BIC;当外心在三角形的外部时,则有∠A=180°- ∠BIC.
∠BIC. 
练习册系列答案
相关题目
 17、如图,在△ABC中,BD是∠ABC的平分线,在△ABC外取一点E,使得∠EAB=∠ACB,AE=DC,并且线段ED与线段AB相交,交点记为K,问线段EK与DK有怎样的大小关系?并说明理由.
17、如图,在△ABC中,BD是∠ABC的平分线,在△ABC外取一点E,使得∠EAB=∠ACB,AE=DC,并且线段ED与线段AB相交,交点记为K,问线段EK与DK有怎样的大小关系?并说明理由.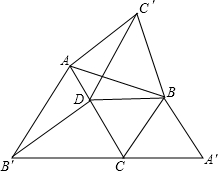 如图,在△ABC中,已知∠DBC=60°,AC>BC,又△ABC′、△BCA′、△CAB′都是△ABC形外的等边三角形,而点D在AC上,且BC=DC
如图,在△ABC中,已知∠DBC=60°,AC>BC,又△ABC′、△BCA′、△CAB′都是△ABC形外的等边三角形,而点D在AC上,且BC=DC
 如图,在△ABC中,D是△ABC外一点,AC=6,BC=8,DH⊥AB于H,且S△ABD=60,DH=12,求∠C的度数.
如图,在△ABC中,D是△ABC外一点,AC=6,BC=8,DH⊥AB于H,且S△ABD=60,DH=12,求∠C的度数. 如图,在△ABC中,BD是∠ABC的平分线,在△ABC外取一点E,使得∠EAB=∠ACB,AE=DC,并且线段ED与线段AB相交,交点记为K,问线段EK与DK有怎样的大小关系?并说明理由.
如图,在△ABC中,BD是∠ABC的平分线,在△ABC外取一点E,使得∠EAB=∠ACB,AE=DC,并且线段ED与线段AB相交,交点记为K,问线段EK与DK有怎样的大小关系?并说明理由.