题目内容
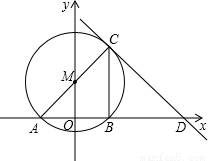
(2006•崇左)如图,在平面直角坐标系中,⊙M与x轴交于A,B两点,AC是⊙M的直径,过点C的直线交x轴于点D,连接BC,已知点M的坐标为 ,直线CD的函数解析式为y=-
,直线CD的函数解析式为y=- x+5
x+5 .
.(1)求点D的坐标和BC的长;
(2)求点C的坐标和⊙M的半径;
(3)求证:CD是⊙M的切线.
【答案】分析:(1)因为点M的坐标为 ,直线CD的函数解析式为y=-
,直线CD的函数解析式为y=- x+5
x+5 ,D在x轴上,可求出OM=
,D在x轴上,可求出OM= ,D(5,0),又因过圆心M的直径⊥AB,AC是直径,利用垂径定理可得OA=OB,AM=MC,∠ABC=90°,利用三角形的中位线可得OM=
,D(5,0),又因过圆心M的直径⊥AB,AC是直径,利用垂径定理可得OA=OB,AM=MC,∠ABC=90°,利用三角形的中位线可得OM= BC,BC=2
BC,BC=2 ;
;
(2)因为BC=2 ,所以可设C(x,2
,所以可设C(x,2 ),利用直线CD的函数解析式为y=-
),利用直线CD的函数解析式为y=- x+5
x+5 .可得到y=-
.可得到y=- x+5
x+5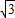 =2
=2 ,即求出C(3,2
,即求出C(3,2 ),利用勾股定理可得AC=
),利用勾股定理可得AC= =
= ,即⊙M的半径为2
,即⊙M的半径为2 ;
;
(3)求出BD=5-3=2,BC= ,CD=
,CD= =4,AC=4
=4,AC=4 ,AD=8,CD=4,
,AD=8,CD=4, ,可得△ACD∽△CBD,
,可得△ACD∽△CBD,
所以∠CBD=∠ACD=90°,CD是⊙M的切线.
解答:(1)解:∵点M的坐标为 ,直线CD的函数解析式为y=-
,直线CD的函数解析式为y=- x+5
x+5 ,D在x轴上,
,D在x轴上,
∴OM= ,D(5,0);
,D(5,0);
∵过圆心M的直径⊥AB,AC是直径,
∴OA=OB,AM=MC,∠ABC=90°,
∴OM= BC,
BC,
∴BC=2 .
.
(2)解:∵BC=2 ,
,
∴设C(x,2 );
);
∵直线CD的函数解析式为y=- x+5
x+5 ,
,
∴y=- x+5
x+5 =2
=2 ,
,
∴x=3,即C(3,2 ),
),
∵CB⊥x轴,OB=3,
∴AO=3,AB=6,AC= =
= ,
,
即⊙M的半径为2 .
.
(3)证明:∵BD=5-3=2,BC= ,CD=
,CD= =4,
=4,
AC=4 ,AD=8,CD=4,
,AD=8,CD=4,
∴ ,
,
∴△ACD∽△CBD,
∴∠CBD=∠ACD=90°;
∵AC是直径,
∴CD是⊙M的切线.
点评:解决本题需用到分类讨论、数形结合、方程和转化等数学思想方法.
 ,直线CD的函数解析式为y=-
,直线CD的函数解析式为y=- x+5
x+5 ,D在x轴上,可求出OM=
,D在x轴上,可求出OM= ,D(5,0),又因过圆心M的直径⊥AB,AC是直径,利用垂径定理可得OA=OB,AM=MC,∠ABC=90°,利用三角形的中位线可得OM=
,D(5,0),又因过圆心M的直径⊥AB,AC是直径,利用垂径定理可得OA=OB,AM=MC,∠ABC=90°,利用三角形的中位线可得OM= BC,BC=2
BC,BC=2 ;
;(2)因为BC=2
 ,所以可设C(x,2
,所以可设C(x,2 ),利用直线CD的函数解析式为y=-
),利用直线CD的函数解析式为y=- x+5
x+5 .可得到y=-
.可得到y=- x+5
x+5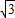 =2
=2 ,即求出C(3,2
,即求出C(3,2 ),利用勾股定理可得AC=
),利用勾股定理可得AC= =
= ,即⊙M的半径为2
,即⊙M的半径为2 ;
;(3)求出BD=5-3=2,BC=
 ,CD=
,CD= =4,AC=4
=4,AC=4 ,AD=8,CD=4,
,AD=8,CD=4, ,可得△ACD∽△CBD,
,可得△ACD∽△CBD,所以∠CBD=∠ACD=90°,CD是⊙M的切线.
解答:(1)解:∵点M的坐标为
 ,直线CD的函数解析式为y=-
,直线CD的函数解析式为y=- x+5
x+5 ,D在x轴上,
,D在x轴上,∴OM=
 ,D(5,0);
,D(5,0);∵过圆心M的直径⊥AB,AC是直径,
∴OA=OB,AM=MC,∠ABC=90°,
∴OM=
 BC,
BC,∴BC=2
 .
.(2)解:∵BC=2
 ,
,∴设C(x,2
 );
);∵直线CD的函数解析式为y=-
 x+5
x+5 ,
,∴y=-
 x+5
x+5 =2
=2 ,
,∴x=3,即C(3,2
 ),
),∵CB⊥x轴,OB=3,
∴AO=3,AB=6,AC=
 =
= ,
,即⊙M的半径为2
 .
.(3)证明:∵BD=5-3=2,BC=
 ,CD=
,CD= =4,
=4,AC=4
 ,AD=8,CD=4,
,AD=8,CD=4,∴
 ,
,∴△ACD∽△CBD,
∴∠CBD=∠ACD=90°;
∵AC是直径,
∴CD是⊙M的切线.
点评:解决本题需用到分类讨论、数形结合、方程和转化等数学思想方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,直线CD的函数解析式为y=-
,直线CD的函数解析式为y=- x+5
x+5 .
.
 ,AF的延长线与DB的延长线交于点P,求证:ED2=EB•EP.
,AF的延长线与DB的延长线交于点P,求证:ED2=EB•EP.

