题目内容
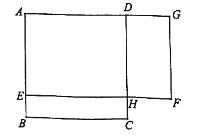
【题目】如图， 
是一块边长为4米的正方形苗圃，园林部门将其改造为矩形
的形状，其中点
在
边上，点
在
的延长线上， 
设
的长为
米，改造后苗圃
的面积为
平方米.
(1) 
与
之间的函数关系式为 （不需写自变量的取值范围）；
(2)根据改造方案，改造后的矩形苗圃
的面积与原正方形苗圃
的面积相等，请问此时
的长为多少米？
【答案】（1）
（或
）；（2）此时
的长为2米
【解析】试题分析：（1）表示出AE、AF，然后根据矩形的面积公式列式整理即可得解；
（2）由原正方形苗圃的面积为16平方米，得
，解一元二次方程即可.
试题解析：（1）E=ABBE=4x，AF=AD+DF=4+2x，
∴y=(4x)(4+2x)=2x2+4x+16，
∵E不与A.B重合，
∴0<x<4，
故y=2x2+4x+16(0<x<4)；
（2）由题意，原正方形苗圃的面积为16平方米，得
解得： 
（不合题意，舍去）.
答：此时
的长为2米
练习册系列答案
相关题目
