题目内容
 如果正方形BEFG的面积为5,正方形ABCD的面积为7,则三角形GCE的面积
如果正方形BEFG的面积为5,正方形ABCD的面积为7,则三角形GCE的面积| 1 |
| 2 |
| 35 |
| 5 |
| 2 |
| 1 |
| 2 |
| 35 |
| 5 |
| 2 |
分析:分别利用两个正方形的面积求的正方形的边长BC和BE的长,然后用三角形CGB的面积减去三角形BGE的面积即可.
解答:解:∵正方形BEFG的面积为5,正方形ABCD的面积为7,
∴BC=
,BG=BE=
,
∴三角形GCE的面为:S△CBG-S△EBG=
BC•BG-
S正方形BEFG=
×
×
-
×5=
-
,
故答案为:
-
∴BC=
| 7 |
| 5 |
∴三角形GCE的面为:S△CBG-S△EBG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 35 |
| 5 |
| 2 |
故答案为:
| 1 |
| 2 |
| 35 |
| 5 |
| 2 |
点评:本题考查了算术平方根的求法,根据正方形的面积求得正方形的边长是进一步解题的基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

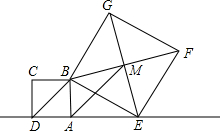 如图,已知正方形ABCD的边长为1,点E是射线DA一动点(DE>1),连结BE,以BE为边在BE上方作正方形BEFG,设M为正方形BEFG的中心,如果定义:只有一组对角是直角的四边形叫做损矩形.
如图,已知正方形ABCD的边长为1,点E是射线DA一动点(DE>1),连结BE,以BE为边在BE上方作正方形BEFG,设M为正方形BEFG的中心,如果定义:只有一组对角是直角的四边形叫做损矩形. 如果正方形BEFG的面积为5,正方形ABCD的面积为7,则三角形GCE的面积________.
如果正方形BEFG的面积为5,正方形ABCD的面积为7,则三角形GCE的面积________.