题目内容
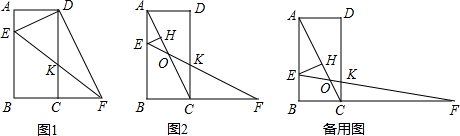
己知矩形ABCD中,对角线AC、BD交于点O,AE⊥BD于E,OE:ED=1:3,AE=2
,AB:AD=
或
或
.
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
分析:作出图形,分①点E在BO上时,根据OE:ED求出点E为BO的中点,然后根据矩形的对角线互相平分且相等求出△ABO是等边三角形,再根据等边三角形的性质求出∠ABO=60°,然后利用60°角的余切值解答;②点E在OD上时,设OE为x,根据比例表示出ED的长,再根据矩形的对角线互相平分且相等表示出BE的长,然后根据相似三角形对应边成比例列出求出x2,再利用勾股定理求出AD、AB的长,即可得解.
解答:解:①如图1,点E在BO上时,
∵四边形ABCD是矩形,
∴OB=OD,
∵OE:ED=1:3,
∴BE=OB-OE=OD-OE=(ED-OE)-OE=3OE-OE-OE=OE,
∴BE=OE,
∴AE∥OB且平分OB,
∴AO=AB(线段垂直平分线上的点到线段两端点的距离相等),
∴△ABO是等边三角形,
∴∠ABO=60°,
∴AB:AD=tan∠ABO=cot60°=
;
②如图2,点E在OD上时,设OE为x,
∵OE:ED=1:3,
∴ED=3x,BE=OE+OB=x+(x+3x)=5x,
由直角三角形的性质,△ADE∽BAE,
∴
=
,
即
=
,
解得x2=
,
在Rt△ADE中,根据勾股定理,AD=
=
=
,
在Rt△ABE中,根据勾股定理,AB=
=
=
,
所以,AB:AD=
:
=
.
综上所述,AB:AD=
或
.
故答案为:
或
.
∵四边形ABCD是矩形,
∴OB=OD,
∵OE:ED=1:3,
∴BE=OB-OE=OD-OE=(ED-OE)-OE=3OE-OE-OE=OE,
∴BE=OE,
∴AE∥OB且平分OB,
∴AO=AB(线段垂直平分线上的点到线段两端点的距离相等),
∴△ABO是等边三角形,

∴∠ABO=60°,
∴AB:AD=tan∠ABO=cot60°=
| ||
| 3 |
②如图2,点E在OD上时,设OE为x,
∵OE:ED=1:3,
∴ED=3x,BE=OE+OB=x+(x+3x)=5x,
由直角三角形的性质,△ADE∽BAE,
∴
| ED |
| AE |
| AE |
| BE |
即
| 3x | ||
2
|
2
| ||
| 5x |
解得x2=
| 4 |
| 5 |
在Rt△ADE中,根据勾股定理,AD=
| ED2+AE2 |
9×
|
| 4 |
| 5 |
| 30 |
在Rt△ABE中,根据勾股定理,AB=
| AB2+AE2 |
25×
|
| 20 |
| 5 |
| 2 |
所以,AB:AD=
| 20 |
| 5 |
| 2 |
| 4 |
| 5 |
| 30 |
| ||
| 3 |
综上所述,AB:AD=
| ||
| 3 |
| ||
| 3 |
故答案为:
| ||
| 3 |
| ||
| 3 |
点评:本题考查了矩形的性质,等边三角形的性质,线段垂直平分线上的点到线段两端点的距离相等的性质,相似三角形的对应边成比例,注意要分情况讨论求解.

练习册系列答案
相关题目
 ,AB:AD=________.
,AB:AD=________.
 ,AB:AD= .
,AB:AD= .