题目内容
如图1,己知矩形ABCD中,BC=2,AB=4,点E从点A出发沿AB方向以每秒1个单位的速度向点B匀速运动,同时点F从点C出发沿BC的延长线方向以每秒2个单位的速度匀速运动,当E运动到点B时,点F停止运动.连接EF交DC于K,连接DE,DF,设运动时间为t秒.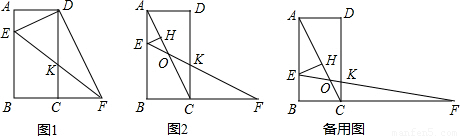
(1)求证:△DAE∽△DCF;
(2)当DK=KF时,求t的值;
(3)如图2,连接AC与EF相交于O,画EH⊥AC于H.
①试探索点E、F在运动过程中,OH的长是否发生改变,若不变,请求出OH的长;若改变,请说明理由.
②当点O是线段EK的三等分点时,直接写出tan∠FOC的值.
【答案】分析:(1)求出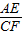 =
=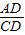 =
= ,∠DAE=∠DCF=90°,根据相似三角形的判定推出即可;
,∠DAE=∠DCF=90°,根据相似三角形的判定推出即可;
(2)根据相似得出∠ADE=∠CDF,求出EK=KF,证△FKC∽△FEB,得出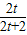 =
= ,求出即可;
,求出即可;
(3)①点E、F在运动过程中,OH的长不变,理由是:作EM∥BC,交AC于M,设∠BAC=α,则tanα= ,得出AE=t,CF=2t,求出EM=
,得出AE=t,CF=2t,求出EM= t,证△MEO∽△CFO,得出
t,证△MEO∽△CFO,得出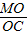 =
=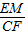 =
= ,求出MO=
,求出MO= CM,设HM=a,则EH=2a,AH=4a,求出MH=
CM,设HM=a,则EH=2a,AH=4a,求出MH= AM,推出OH=
AM,推出OH= AC,求出AC即可求出OH;②tan∠FOC的值是
AC,求出AC即可求出OH;②tan∠FOC的值是 或
或 ,理由是:根据△FKC∽△FEB求出KC=
,理由是:根据△FKC∽△FEB求出KC=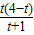 ,根据△CKO∽△AEO得出
,根据△CKO∽△AEO得出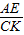 =
=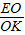 ,当
,当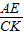 =
=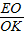 =
= 时得出
时得出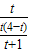 =2,求出t,即可得出AE长,根据△AEH∽△ACB,求出EH,当
=2,求出t,即可得出AE长,根据△AEH∽△ACB,求出EH,当 =
=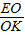 =
= 时得出
时得出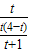 =
= ,求出t,根据△AEH∽△ACB,求出EH的值,解直角三角形求出即可.
,求出t,根据△AEH∽△ACB,求出EH的值,解直角三角形求出即可.
解答:解:(1)由题意,得AE=t,CF=2t.
∵矩形ABCD中,BC=AD=2,AB=CD=4,
∴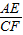 =
=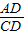 =
= ,
,
∵∠DAE=∠DCF=90°,
∴△DAE∽△DCF;
(2)∵△DAE∽△DCF,
∴∠ADE=∠CDF,
∵∠ADE+∠EDC=90°,
∴∠CDF+∠EDC=90°,即∠EDF=90°,
∵DK=KF,
∴∠KDF=∠KFD,
∵∠DEK+∠KFD=90°,∠EDK+∠KDF=90°,
∴∠DEK=∠EDK,
∴DK=EK,
∴EK=KF,
∵AB∥CD,
∴△FKC∽△FEB,
∴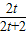 =
= ,
,
t=1;
(3)①点E、F在运动过程中,OH的长不变,
理由是:作EM∥BC,交AC于M,设∠BAC=α,则tanα= ,
,
∵AB⊥BC,
∴ME⊥AB,
∵AB⊥AC,
∴∠HEM=α,
∵AE=t,CF=2t,
∴EM= t,
t,
∵∠EOM=∠FOC,∠MEO=∠CFO,
∴△MEO∽△CFO,
∴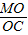 =
=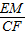 =
= ,
,
∴MO= OC,
OC,
∴MO= CM,
CM,
设HM=a,则EH=2a,AH=4a,
∴MH= AM,
AM,
∴OH=OM+MH= CM+
CM+ AM=
AM= AC,
AC,
在Rt△ABC中,AB=4,BC=2,由勾股定理得:AC=2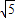 ,
,
∴OH= ,
,
即点E、F在运动过程中,OH的长度不变,是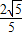 ;
;
②tan∠FOC的值是 或
或 ,
,
理由是:∵四边形ABCD是矩形,
∴CD∥AB,
∴△FKC∽△FEB,
∴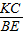 =
=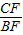 ,
,
∴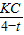 =
=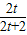 ,
,
∴KC= ,
,
∵AB∥CD,
∴△CKO∽△AEO,
∴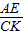 =
= ,
,
当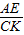 =
=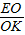 =
= 时,
时,
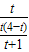 =2,
=2,
t=0(舍去),t= ,
,
∵EH⊥AC,
∴∠EHA=∠ABC=90°,
∵∠EAH=∠BAC,
∴△AEH∽△ACB,
∴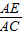 =
=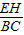 ,
,
∴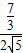 =
=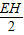 ,
,
∴EH=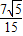 ,
,
∴tan∠FOC=tan∠EOH= =
=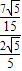 =
= ;
;
当 =
=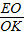 =
= 时,
时,
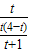 =
= ,
,
t=0(舍去),t= ,
,
∵EH⊥AC,
∴∠EHA=∠ABC=90°,
∵∠EAH=∠BAC,
∴△AEH∽△ACB,
∴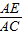 =
=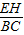 ,
,
∴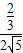 =
=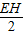 ,
,
∴EH=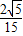 ,
,
∴tan∠FOC=tan∠EOH=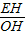 =
=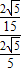 =
= .
.
点评:本题考查了相似三角形的性质和判定,矩形性质和判定,直接直角三角形的应用,主要考查学生的推理能力,题目比较好,但是难度偏大.
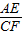 =
=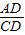 =
= ,∠DAE=∠DCF=90°,根据相似三角形的判定推出即可;
,∠DAE=∠DCF=90°,根据相似三角形的判定推出即可;(2)根据相似得出∠ADE=∠CDF,求出EK=KF,证△FKC∽△FEB,得出
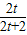 =
= ,求出即可;
,求出即可;(3)①点E、F在运动过程中,OH的长不变,理由是:作EM∥BC,交AC于M,设∠BAC=α,则tanα=
 ,得出AE=t,CF=2t,求出EM=
,得出AE=t,CF=2t,求出EM= t,证△MEO∽△CFO,得出
t,证△MEO∽△CFO,得出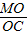 =
=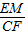 =
= ,求出MO=
,求出MO= CM,设HM=a,则EH=2a,AH=4a,求出MH=
CM,设HM=a,则EH=2a,AH=4a,求出MH= AM,推出OH=
AM,推出OH= AC,求出AC即可求出OH;②tan∠FOC的值是
AC,求出AC即可求出OH;②tan∠FOC的值是 或
或 ,理由是:根据△FKC∽△FEB求出KC=
,理由是:根据△FKC∽△FEB求出KC=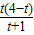 ,根据△CKO∽△AEO得出
,根据△CKO∽△AEO得出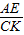 =
=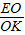 ,当
,当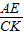 =
=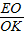 =
= 时得出
时得出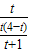 =2,求出t,即可得出AE长,根据△AEH∽△ACB,求出EH,当
=2,求出t,即可得出AE长,根据△AEH∽△ACB,求出EH,当 =
=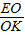 =
= 时得出
时得出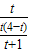 =
= ,求出t,根据△AEH∽△ACB,求出EH的值,解直角三角形求出即可.
,求出t,根据△AEH∽△ACB,求出EH的值,解直角三角形求出即可.解答:解:(1)由题意,得AE=t,CF=2t.
∵矩形ABCD中,BC=AD=2,AB=CD=4,
∴
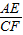 =
=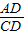 =
= ,
,∵∠DAE=∠DCF=90°,
∴△DAE∽△DCF;
(2)∵△DAE∽△DCF,
∴∠ADE=∠CDF,
∵∠ADE+∠EDC=90°,
∴∠CDF+∠EDC=90°,即∠EDF=90°,
∵DK=KF,
∴∠KDF=∠KFD,
∵∠DEK+∠KFD=90°,∠EDK+∠KDF=90°,
∴∠DEK=∠EDK,
∴DK=EK,
∴EK=KF,
∵AB∥CD,
∴△FKC∽△FEB,
∴
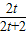 =
= ,
,t=1;
(3)①点E、F在运动过程中,OH的长不变,
理由是:作EM∥BC,交AC于M,设∠BAC=α,则tanα=
 ,
,
∵AB⊥BC,
∴ME⊥AB,
∵AB⊥AC,
∴∠HEM=α,
∵AE=t,CF=2t,
∴EM=
 t,
t,∵∠EOM=∠FOC,∠MEO=∠CFO,
∴△MEO∽△CFO,
∴
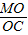 =
=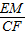 =
= ,
,∴MO=
 OC,
OC,∴MO=
 CM,
CM,设HM=a,则EH=2a,AH=4a,
∴MH=
 AM,
AM,∴OH=OM+MH=
 CM+
CM+ AM=
AM= AC,
AC,在Rt△ABC中,AB=4,BC=2,由勾股定理得:AC=2
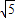 ,
,∴OH=
 ,
,即点E、F在运动过程中,OH的长度不变,是
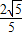 ;
;②tan∠FOC的值是
 或
或 ,
,理由是:∵四边形ABCD是矩形,
∴CD∥AB,
∴△FKC∽△FEB,
∴
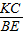 =
=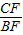 ,
,∴
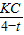 =
=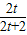 ,
,∴KC=
 ,
,∵AB∥CD,
∴△CKO∽△AEO,
∴
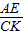 =
= ,
,当
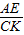 =
=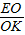 =
= 时,
时,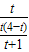 =2,
=2,t=0(舍去),t=
 ,
,∵EH⊥AC,
∴∠EHA=∠ABC=90°,
∵∠EAH=∠BAC,
∴△AEH∽△ACB,
∴
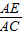 =
=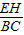 ,
,∴
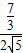 =
=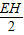 ,
,∴EH=
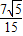 ,
,∴tan∠FOC=tan∠EOH=
 =
=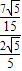 =
= ;
;当
 =
=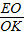 =
= 时,
时,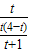 =
= ,
,t=0(舍去),t=
 ,
,∵EH⊥AC,
∴∠EHA=∠ABC=90°,
∵∠EAH=∠BAC,
∴△AEH∽△ACB,
∴
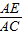 =
=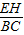 ,
,∴
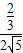 =
=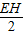 ,
,∴EH=
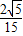 ,
,∴tan∠FOC=tan∠EOH=
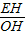 =
=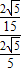 =
= .
.点评:本题考查了相似三角形的性质和判定,矩形性质和判定,直接直角三角形的应用,主要考查学生的推理能力,题目比较好,但是难度偏大.

练习册系列答案
相关题目
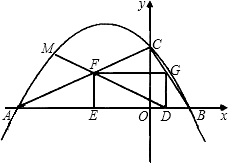 抛物线对称轴为直线x=-3.
抛物线对称轴为直线x=-3.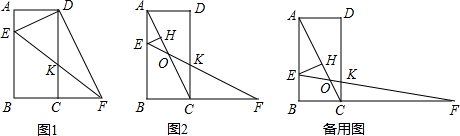
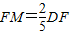 ,求出此时点M的坐标;
,求出此时点M的坐标;
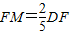 ,求出此时点M的坐标;
,求出此时点M的坐标;