题目内容
如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图像被⊙P截得的弦AB的长为2 ,则a的值是( )
,则a的值是( )

 ,则a的值是( )
,则a的值是( )
A.2 | B.2+ | C.2 | D.2+ |
B
过P点作PE⊥AB于E,过P点作PC⊥x轴于C,交AB于D,连接PA.
∵PE⊥AB,AB=2 ,半径为2,
,半径为2,
∴AE= AB=
AB= ,PA=2,
,PA=2,
根据勾股定理得:PE= =1,
=1,
∵点A在直线y=x上,
∴∠AOC=45°,
∵∠DCO=90°,
∴∠ODC=45°,
∴△OCD是等腰直角三角形,
∴OC=CD=2,
∴∠PDE=∠ODC=45°,
∴∠DPE=∠PDE=45°,
∴DE=PE=1,
∴PD=
∵⊙P的圆心是(2,a),
∴a=PD+DC=2+ .
.
故选B.
∵PE⊥AB,AB=2
 ,半径为2,
,半径为2,∴AE=
 AB=
AB= ,PA=2,
,PA=2,根据勾股定理得:PE=
 =1,
=1,∵点A在直线y=x上,
∴∠AOC=45°,
∵∠DCO=90°,
∴∠ODC=45°,
∴△OCD是等腰直角三角形,
∴OC=CD=2,
∴∠PDE=∠ODC=45°,
∴∠DPE=∠PDE=45°,
∴DE=PE=1,
∴PD=

∵⊙P的圆心是(2,a),
∴a=PD+DC=2+
 .
.故选B.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
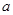 的正三角形的外接圆的半径为 .
的正三角形的外接圆的半径为 .
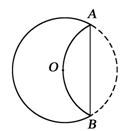
 , 则劣弧
, 则劣弧  的长 是 .
的长 是 . 
 的度数为
的度数为 ,
, 的度数为
的度数为 ,则 PC+PD的最小值是_____ 。
,则 PC+PD的最小值是_____ 。 

