题目内容
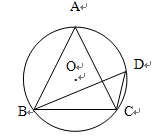
如图,设半径为3的半圆⊙O,直径为AB,C、D为半圆上的两点,P点是AB上一动点,若  的度数为
的度数为 ,
, 的度数为
的度数为 ,则 PC+PD的最小值是_____ 。
,则 PC+PD的最小值是_____ 。
 的度数为
的度数为 ,
, 的度数为
的度数为 ,则 PC+PD的最小值是_____ 。
,则 PC+PD的最小值是_____ 。  |


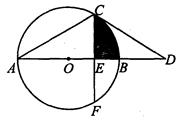
解:设点D关于AB的对称点为E,连接CE交AB于P,则此时PC+PD的值最小,且PC+PD=PC+PE=CE.连接OC、OE;
∵
 的度数为
的度数为 ,
, 的度数为
的度数为 ,
,∴弧CD的度数为48°;
∴弧CBE的度数为120°,即∠COE=120°;
过O作OF⊥CE于F,则∠COF=60°;
Rt△OCF中,OC=1,∠COF=60°;因此CF=
 ;
;∴CE=2CF=

即PC+PD的最小值为
 。
。根据作法知弧CE的度数是120°,即∠COE=120°,作OF⊥CE于F;
在Rt△OCF中,∠OCF=30°,OC=1,即可求出CF和CE的长,也就求出了PC+PD的最小值。

练习册系列答案
相关题目
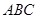 与⊙
与⊙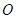 等高,如图放置, ⊙
等高,如图放置, ⊙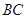 相切于点
相切于点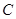 ,⊙
,⊙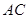 相交于点
相交于点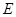 ,则
,则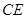 的长为 ㎝.
的长为 ㎝.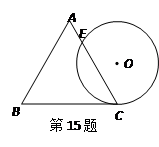
 ,则a的值是( )
,则a的值是( )

 是⊙O的直径,把
是⊙O的直径,把 为
为 的直角三角板
的直角三角板 的一条直角边
的一条直角边 放在直线
放在直线 与⊙O交于点
与⊙O交于点 ,点
,点 与点
与点 重合.将三角板
重合.将三角板 方向平移,使得点
方向平移,使得点 重合为止.设
重合为止.设 ,则
,则 的取值范围是( )
的取值范围是( )





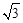 ,
,