��Ŀ����
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A������Ϊ����8��0������B������Ϊ����8��6����ֱ��BC��x�ᣬ��y���ڵ�C�����ı���OABC�Ƶ�O��˳ʱ�뷽����ת���ȵõ��ı���OA��B��C�䣬��ʱֱ��OA�䡢ֱ��B��C��ֱ���ֱ��BC�ཻ�ڵ�P��Q��
��1���ı���OABC����״�� �� ����=90��ʱ�� ![]() ��ֵ�� ��
��ֵ�� ��
��2������ͼ2�����ı���OA��B��C��Ķ���B������y����������ʱ���� ![]() ��ֵ��
��ֵ��
����ͼ3�����ı���OA��B��C��Ķ���B������BC���ӳ�����ʱ�����OPB��������

��3�����ı���OABC��ת�����У���0�㣼����180��ʱ���Ƿ���������ĵ�P�͵�Q��ʹBP= ![]() BQ�������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
BQ�������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1������![]()
��2��
�⣺��ͼ2��
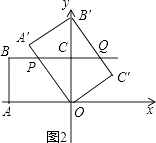
�ߡ�POC=��B��OA�䣬��PCO=��OA��B��=90�㣬
���COP�ס�A��OB�䣮
�� ![]() ����
���� ![]() ��
��
��CP= ![]() ��BP=BC��CP=
��BP=BC��CP= ![]() ��
��
ͬ����B��CQ�ס�B��C��O��
�� ![]() ��
��
�� ![]()
��CQ=3��BQ=BC+CQ=11��
�� 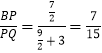 ��
��
�� ![]() ��
��
��ͼ3���ڡ�OCP�͡�B��A��P�У� 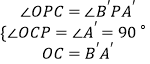 ��
��
���OCP�ա�B��A��P��AAS����
��OP=B��P��
��B��P=x��
��Rt��OCP����8��x��2+62=x2��
���x= ![]() ��
��
��S��OPB��= ![]() ��
�� ![]() ��6=
��6= ![]()
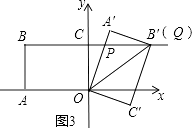
��3��
�⣺���������ĵ�P�͵�Q��ʹBP= ![]() BQ��
BQ��
��P��������P1����9�� ![]() ��6����P2����
��6����P2���� ![]() ��6����
��6����
���ɣ�
����Q��QH��OA����H������OQ����QH=OC��=OC��
��S��POQ= ![]() PQOC��S��POQ=
PQOC��S��POQ= ![]() OPQH��
OPQH��
��PQ=OP��
��BP=x��
��BP= ![]() BQ��
BQ��
��BQ=2x��
��ͼ4������P�ڵ�B���ʱ��
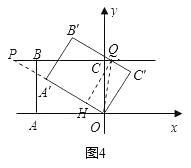
OP=PQ=BQ+BP=3x��
��Rt��PCO����8+x��2+62=��3x��/span>2��
���x1=1+ ![]() ��x2=1��
��x2=1�� ![]() ������ʵ�ʣ���ȥ����
������ʵ�ʣ���ȥ����
��PC=BC+BP=9+ ![]() ��
��
��P����9�� ![]() ��6����
��6����
��ͼ5������P�ڵ�B�Ҳ�ʱ��
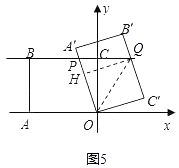
��OP=PQ=BQ��BP=x��PC=8��x��
��Rt��PCO����8��x��2+62=x2�����x= ![]() ��
��
��PC=BC��BP=8�� ![]() =
= ![]() ��
��
��P���� ![]() ��6����
��6����
���Ͽ�֪�����ڵ�P����9�� ![]() ��6����
��6���� ![]() ��6����ʹBP=
��6����ʹBP= ![]() BQ��
BQ��
���������⣺��1��ͼ1���ı���OA��B��C�����״�Ǿ��Σ�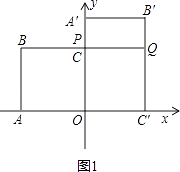
�ߵ�A������Ϊ����8��0������B����8��6����
��AB��OC��
��BC��x�ᣬ
���ı���OABC��ƽ���ı��Σ�
��OC��OA��
��ƽ���ı���OABC����״�Ǿ��Σ�
����=90��ʱ��P��C�غϣ���ͼ1��
BP=8��BQ=BP+OC=8+6=14��
�� ![]() ��
��
���Ǿ��εij�����ıȣ��� ![]() ��
��
���Դ��Ǿ��Σ� ![]() ��
��

 �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д� ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�