题目内容
 如图所示,△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且BE=AC.求证:DE=CD.
如图所示,△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且BE=AC.求证:DE=CD.分析:求出∠EDB=∠CDA=90°,求出∠BAD=∠ABD=45°,推出BD=AD,根据HL证出Rt△BDE≌Rt△ADC即可.
解答:证明:∵AD⊥BC,
∴∠EDB=∠CDA=90°,
∵∠ABC=45°,
∴∠BAD=∠ABD=45°,
∴BD=AD,
在Rt△BDE和Rt△ADC中
∴Rt△BDE≌Rt△ADC(HL),
∴DE=CD.
∴∠EDB=∠CDA=90°,
∵∠ABC=45°,
∴∠BAD=∠ABD=45°,
∴BD=AD,
在Rt△BDE和Rt△ADC中
|
∴Rt△BDE≌Rt△ADC(HL),
∴DE=CD.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的对应边相等.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
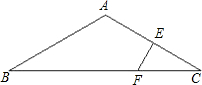 如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.
如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF. 16、如图所示,△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、AC于D、E,∠CAE:∠EAB=5:2,则∠B=
16、如图所示,△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、AC于D、E,∠CAE:∠EAB=5:2,则∠B=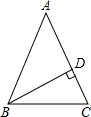 如图所示,△ABC中,AB=AC=10,BD是AC边的高线,DC=2,试求BD的长.
如图所示,△ABC中,AB=AC=10,BD是AC边的高线,DC=2,试求BD的长. 如图所示,△ABC中,BC的垂直平分线交AB于点E,若△ABC的周长为10,BC=4,则△ACE的周长是
如图所示,△ABC中,BC的垂直平分线交AB于点E,若△ABC的周长为10,BC=4,则△ACE的周长是 如图所示,△ABC中,AB=AC,BD⊥AC,垂足为D,求∠DBC与∠A的关系.
如图所示,△ABC中,AB=AC,BD⊥AC,垂足为D,求∠DBC与∠A的关系.