题目内容
如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A、C分别在x轴、y轴的正半轴,抛物线y=﹣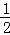 x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.
x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和四边形ABCD的面积.
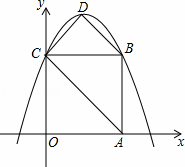
解:(1)由已知得:C(0,4),B(4,4),
把B与C坐标代入y=﹣ x2+bx+c得:
x2+bx+c得: ,
,
解得:b=2,c=4,
则解析式为y=﹣ x2+2x+4;
x2+2x+4;
(2)∵y=﹣ x2+2x+4=﹣
x2+2x+4=﹣ (x﹣2)2+6,
(x﹣2)2+6,
∴抛物线顶点坐标为(2,6),
则S四边形ABDC= S△ABC+S△BCD=
S△ABC+S△BCD= ×4×4+
×4×4+ ×4×2=8+4=12.
×4×2=8+4=12.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 我”字所在面的位置关系是( )
我”字所在面的位置关系是( )
 (米)
(米) 和所经过的时间
和所经过的时间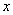 (分)之间的函数图象如
(分)之间的函数图象如 图所示。请根据图象回答下列问题:
图所示。请根据图象回答下列问题: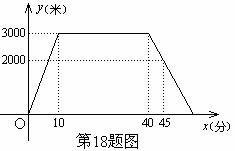
 有实数根,则a的取值范围是
有实数根,则a的取值范围是 B.
B.
 D.
D.
 ,分别以OC,OA 所在的直线为x 轴,y 轴建立平面直角坐标系.
,分别以OC,OA 所在的直线为x 轴,y 轴建立平面直角坐标系.