题目内容
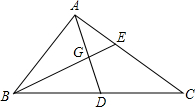
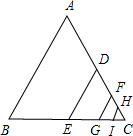
如图,在△ABC中,AM与BN相交于D,BM=3MC,AD=DM,求:
(1)BD:DN的值;
(2)面积S△ABN:S△CBN的值.

(1)BD:DN的值;
(2)面积S△ABN:S△CBN的值.

(1)过C作CE∥AM交BA延长线于点E,延长BN交CE于点F.
∵CE∥AM,
∴∠DAN=∠FCN,∠ADN=∠CFN,
∴△DAN∽△FCN,
∴
=
,
又∵AD=DM,
∴
=
,
∵CE∥AM,
∴
=
=
=
,
∴
=
,
∴BD:DN=3:
=7:1.
(2)由(1)得:△DAN相似于△FCN,
∴
=
=
∴S△ABN:S△CBN=AN:CN=3:4.

∵CE∥AM,
∴∠DAN=∠FCN,∠ADN=∠CFN,
∴△DAN∽△FCN,
∴
| DN |
| FN |
| AD |
| CF |
又∵AD=DM,
∴
| DN |
| FN |
| DM |
| CF |
∵CE∥AM,
∴
| BD |
| BF |
| DM |
| FC |
| BM |
| BC |
| 3 |
| 4 |
∴
| DN |
| FN |
| 3 |
| 4 |
∴BD:DN=3:
| 3 |
| 7 |
(2)由(1)得:△DAN相似于△FCN,
∴
| AN |
| CN |
| DN |
| FN |
| 3 |
| 4 |
∴S△ABN:S△CBN=AN:CN=3:4.


练习册系列答案
相关题目