��Ŀ����
��ͼ����ABC �ı� BC ��ֱ�� l �ϣ�AD ����ABC �ĸߣ���ABC=45�㣬BC=6cm��AB=2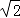 cm���� P �ӵ� B ������ BC ������ 1cm/s �ٶ���� C �˶������� P ���� C ʱ��ֹͣ�˶���PQ��BC��PQ �� AB �� AC �ڵ� Q���� PQ Ϊһ�����Ҳ������� PQRS��PS=2PQ������ PQRS ����ABC ���ص����� �����Ϊ S��cm2������ P ���˶�ʱ��Ϊ t��s�����ش��������⣺
cm���� P �ӵ� B ������ BC ������ 1cm/s �ٶ���� C �˶������� P ���� C ʱ��ֹͣ�˶���PQ��BC��PQ �� AB �� AC �ڵ� Q���� PQ Ϊһ�����Ҳ������� PQRS��PS=2PQ������ PQRS ����ABC ���ص����� �����Ϊ S��cm2������ P ���˶�ʱ��Ϊ t��s�����ش��������⣺
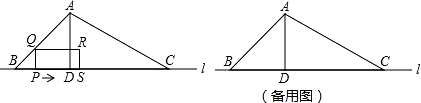
��1��AD= 2 cm��
���� R �ڱ� AC ��ʱ���� t ��ֵ��
��3���� S �� t ֮��ĺ�����ϵʽ��
�����㡿�������ۺ��⣮
����������1���� AD ����ABC �ĸߣ���ABC=45�㣬�ɵ� AD=BD������ AB=2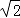 cm�����ɵó� AD
cm�����ɵó� AD
�ij���
���� QR��BC����֤����AQR�ס�ABC���Ӷ��ó�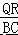 =
= 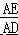 ����
����  =
= 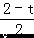 ����� t ���ɣ�
����� t ���ɣ�
��3�������ν������ۣ�
�ٵ� 0��t��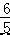 ʱ��ͼ 1����������B=45�㣬��BPQ=90�㣬���ɵó���BQP=45�㣬�� PQ=BP=t���Ӷ��ó� S �� t ֮��ĺ�����ϵʽ��
ʱ��ͼ 1����������B=45�㣬��BPQ=90�㣬���ɵó���BQP=45�㣬�� PQ=BP=t���Ӷ��ó� S �� t ֮��ĺ�����ϵʽ��

��ϰ��ϵ�д�
�����Ŀ
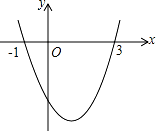
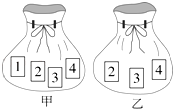
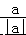 ���ĸ����У������ĸ����� ��
���ĸ����У������ĸ����� ��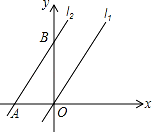
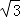 A��3 B��4 C��2
A��3 B��4 C��2 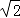 D��2
D��2