Question

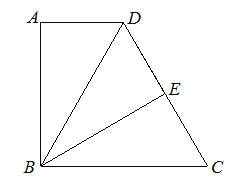
【题目】如图，在平行四边形中，，，点是的中点，连接，过作于，交于点，点是的中点，连接，过点作的垂线交的延长线于．

（1）若，的长；

（2）求证：．

Answer 1

【答案】（1）DP＝；（2）见解析．

【解析】

（1）过P作PM⊥BD于M，根据角平分线的性质得PM＝PF，证明Rt△BFP≌R△BMP（HL），得BM＝BF＝，求出DM＝，根据等腰直角三角形的性质可得结论；

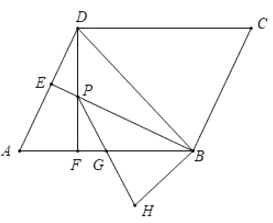
（2）连接AP，构建全等三角形，先证明△ADF≌△PBF（ASA），得PF＝AF，再证明△APG≌△BHG（ASA），得BH＝AP，求出∠ADP＝∠DAP＝22.5°得AP＝DP，从而得结论．

解：（1）如图，过P作PM⊥BD于M，

∵四边形ABCD是平行四边形，

∴CD＝AB＝BD＝4，

∵E是AD的中点，

∴∠DBE＝∠ABE，

∵PF⊥AB，PM⊥BD，

∴PF＝PM，

∵∠ABD＝45°，

∴△BDF是等腰直角三角形，

∴DF＝BF＝，∠BDF＝45°，

∴DM＝PM，PD＝DM，

在Rt△BFP和Rt△BMP中，

∵PF＝PM，BP＝BP，

∴Rt△BFP≌Rt△BMP（HL），

∴BM＝BF＝，

∴DM＝，

∴DP＝DM＝；

（2）连接AP，

∵∠DEP＝∠PFB＝90°，∠EPD＝∠FPB，

∴∠EDP＝∠FBP，

又∵DF＝BF，∠AFD＝∠BFP＝90°，

∴△ADF≌△PBF（ASA），

∴PF＝AF，

∴∠PAF＝45°，

∵BD⊥BH，

∴∠DBH＝90°，

∵∠DBF＝45°，

∴∠HBG＝90°45°＝45°，

∴∠PAF＝∠HBG，

又∵AG＝BG，∠PGA＝∠HGB，

∴△APG≌△BHG（ASA），

∴BH＝AP，

∵AB＝BD，∠ABD＝45°，

∴∠DAB＝∠ADB＝67.5°，

∴∠ADP＝∠DAP＝22.5°，

∴AP＝DP，

∴．